Mientras todos pretenden escapar de las matemáticas por utilizar un lenguaje tan abstracto que no llena de frente las realidades materiales del cerebro en forma directa, algunos estudiantes encuentran en esta forma de expresar el conocimiento y la realidad que nos rodea …FASCINANTE!!
MODELAR la realidad es el objetivo principal de la matemáticas. En el siguiente curso te presentaremos los esquemas básicos aplicados a la física de la matemáticas en su forma ALGEBRAICA.
¿ Hasta donde puede modelar el mundo la matemática?
ÁLGEBRA INICIAL : GRADO OCTAVO
Bienvenidos estudiantes, con el fin de fundamentar elementos de matemáticas necesarios para el desarrollo de la FÍSICA 1 y 2, estas BASES apoyadas en los derechos básicos de aprendizaje para GRADO OCTAVO nos pueden ser muy útiles.
Inicialmente revisemos los derechos básicos de aprendizaje en MATEMÁTICAS para GRADO OCTAVO :
DERECHOS BÁSICOS DE APRENDIZAJE GRADO OCTAVO:
Reconoce la existencia de los números irracionales como números no racionales y los describe de acuerdo con sus características y propiedades.
Evidencias de aprendizaje
- Utiliza procedimientos geométricos para representar números racionales e irracionales.
- Identifica las diferentes representaciones (decimales y no decimales) para argumentar por qué un número es o no racional
Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
Evidencias de aprendizaje
- Utiliza procedimientos geométricos o aritméticos para construir algunos números irracionales y los ubica en la recta numérica.
- Justificar procedimientos con los cuales se representa geométricamente números racionales y números reales.
- Construye varias representaciones (geométrica, decimales o no decimales) de un mismo número racional o irracional.
Reconoce los diferentes usos y significados de las operaciones (convencionales y no convencionales) y del signo igual (relación de equivalencia e igualdad condicionada) y los utiliza para argumentar equivalencias entre expresiones algebraicas y resolver sistemas de ecuaciones.
Evidencias de aprendizaje
- Reconoce el uso del signo igual como relación de equivalencia de expresiones algebraicas en los números reales.
- Propone y ejecuta procedimientos para resolver una ecuación lineal y sistemas de ecuaciones lineales y argumenta la validez o no de un procedimiento
- Usa el conjunto solución de una relación (de equivalencia y de orden) para argumentar la validez o no de un procedimiento.
Describe atributos medibles de diferentes sólidos y explica relaciones entre ellos por medio del lenguaje algebraico.
Evidencias de aprendizaje
- Utiliza lenguaje algebraico para representar el volumen de un prisma en términos de sus aristas.
- Realiza la representación gráfica del desarrollo plano de un prisma.
- Estima, calcula y compara volúmenes a partir de las relaciones entre las aristas de un prisma o de otros sólidos.
- Interpreta las expresiones algebraicas que representan el volumen y el área cuando sus dimensiones varían.
Utiliza y explica diferentes estrategias para encontrar el volumen de objetos regulares e irregulares en la solución de problemas en las matemáticas y en otras ciencias.
Evidencias de aprendizaje
- Estima medidas de volumen con unidades estandarizadas y no estandarizadas.
Utiliza la relación de las unidades de capacidad con las unidades de volumen (litros, dm3, etc) en la solución de un problema. - Identifica la posibilidad del error en la medición del volumen haciendo aproximaciones pertinentes al respecto.
- Explora y crea estrategias para calcular el volumen de cuerpos regulares e irregulares.
Identifica relaciones de congruencia y semejanza entre las formas geométricas que configuran el diseño de un objeto.
Evidencias de aprendizaje
- Utiliza criterios para argumentar la congruencia de dos triángulos.
- Discrimina casos de semejanza de triángulos en situaciones diversas.
- Resuelve problemas que implican aplicación de los criterios de semejanza.
- Compara figuras y argumenta la posibilidad de ser congruente o semejantes entre sí.
Identifica regularidades y argumenta propiedades de figuras geométricas a partir de teoremas y las aplica en situaciones reales.
Evidencias de aprendizaje
- Describe teoremas y argumenta su validez a través de diferentes recursos (Software, tangram, papel, entre otros).
- Argumenta la relación pitagórica por medio de construcción al utilizar material concreto.
- Reconoce relaciones geométricas al utilizar el teorema de Pitágoras y Thales, entre otros.
- Aplica el teorema de Pitágoras para calcular la medida de cualquier lado de un triángulo rectángulo.
- Resuelve problemas utilizando teoremas básicos.
Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
Evidencias de aprendizaje
- Opera con formas simbólicas y las interpreta.
- Relaciona un cambio en la variable independiente con el cambio correspondiente en la variable dependiente.
- Encuentra valores desconocidos en ecuaciones algebraicas.
- Reconoce y representa relaciones numéricas mediante expresiones algebraicas y encuentra el conjunto de variación de una variable en función del contexto.
Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.
Evidencias de aprendizaje
- Opera con formas simbólicas que representan números y encuentra valores desconocidos en ecuaciones numéricas.
- Reconoce patrones numéricos y los describe verbalmente.
- Representa relaciones numéricas mediante expresiones algebraicas y opera con y sobre variables.
- Describe diferentes usos del signo igual (equivalencia, igualdad condicionada) en las expresiones algebraicas.
- Utiliza las propiedades de los conjuntos numéricos para resolver ecuaciones.
Propone relaciones o modelos funcionales entre variables e identifica y analiza propiedades de covariación entre variables, en contextos numéricos, geométricos y cotidianos y las representa mediante gráficas (cartesianas de puntos, continuas, formadas por segmentos, etc.).
Evidencias de aprendizaje
- Toma decisiones informadas en exploraciones numéricas, algebraicas o gráficas de los modelos matemáticos usados.
- Relaciona características algebraicas de las funciones, sus gráficas y procesos de aproximación sucesiva.
Interpreta información presentada en tablas de frecuencia y gráficos cuyos datos están agrupados en intervalos y decide cuál es la medida de tendencia central que mejor representa el comportamiento de dicho conjunto.
Evidencias de aprendizaje
- Interpreta los datos representados en diferentes tablas y gráficos.
- Usa estrategias gráficas o numéricas para encontrar las medidas de tendencia central de un conjunto de datos agrupados.
- Describe el comportamiento de los datos empleando las medidas de tendencia central y el rango.
- Reconoce cómo varían las medidas de tendencia central y el rango cuando varían los datos.
Hace predicciones sobre la posibilidad de ocurrencia de un evento compuesto
e interpreta la predicción a partir del uso de propiedades básicas de la probabilidad.
Evidencias de aprendizaje
- Identifica y enumera el espacio muestral de un experimento aleatorio.
- Identifica y enumera los resultados favorables de ocurrencia de un evento indicado.
- Asigna la probabilidad de la ocurrencia de un evento usando valores entre 0 y 1.
- Reconoce cuando dos eventos son o no mutuamente excluyentes y les asigna la
probabilidad usando la regla de la adición.
Cartilla de enseñanza del ministerio de educación
En el siguiente enlace podrás encontrar y descargar la cartilla básica para nivel octavo de aprendizaje elaborada por el ministerio de Educación:
NUESTRO TEXTO GUÍA ADICIONAL:
NUESTRO TEXTO DE LECTURA:
PLAN DE TRABAJO
| Temáticas (semanas) | Contenidos |
| LAS ECUACIONES COMO FORMA DE MODELAR LA NATURALEZA
(Trabajando la CANTIDAD, EL ESPACIO Y LA FORMA) |
ECUACIONES Y ORÍGENES
· Los inicios del álgebra. El espacio numérico (Racionales e Irracionales) · La escritura y el álgebra . Los problemas y las ecuaciones en contexto |
| OPERACIONES CON ECUACIONES
· Sustitución y Valor real · Reducción · Suma y Resta · Multiplicación y División · Despeje de incógnitas . Solución de ecuaciones de primer grado PROBLEMAS CON ECUACIONES · Situaciones que implican sumas y restas. · Situaciones que implican multiplicación y división. · Situaciones que implican potenciación y radicación.
|
|
| SIMPLIFICANDO LAS ECUACIONES
(Trabajando EL CAMBIO Y LAS RELACIONES) |
FACTORIZACIÓN |
| LA GEOMETRÍA DEL ÁLGEBRA
(Trabajando EL CAMBIO Y LAS RELACIONES) |
La naturaleza: entorno geométrico de las matemáticas |
| Principios de geometría plana, sistemas de medición. Area y Volumen. Congruencia y Semejanza. | |
| Teoremas de Thales y de Pitágoras | |
| Gráficas en el plano cartesiano. | |
| ESTADÍSTICA Y PROBABILIDADES
(Trabajando la INCERTIDUMBRE) |
Tablas de Frecuencia. Media, moda y mediana.
Probabilidad básica. |
Las ecuaciones como forma de modelar la naturaleza
EL ORIGEN DEL ÁLGEBRA
Hablar del álgebra es hablar del origen del pensamiento humano y su capacidad para interrogarse acerca de su entorno.
Prácticamente desde sus primeros descubrimientos y su necesidad de manipular la naturaleza nace el deseo de mantener un control numérico de su realidad.

Este deseo de contabilizar la naturaleza aparece en la medida que el hombre deja de desplazarse en la tierra y se hace sedentario fundando las primeras culturas del periodo neolítico.

Uno de los primeros interrogantes del hombre será el tiempo y sus periodos. Observar las crecientes de los ríos, el paso de las estaciones, las épocas de siembra y cosecha, las épocas de migración de los animales, etc…llevan al hombre a crear un sistema de manejo para el tiempo que más adelante se conocerá como calendario.
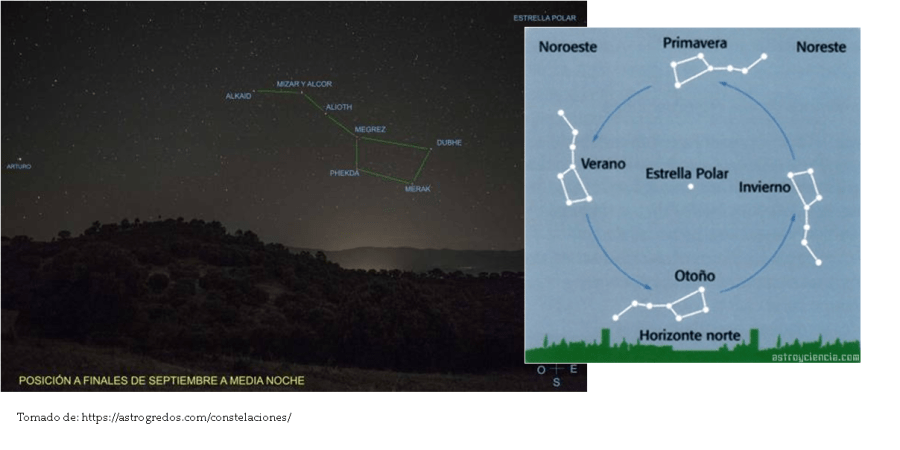
El hombre observa una regularidad en las épocas y el movimiento de las estrellas, que más adelante va a relacionar con su sistema de medición basado en medidas y contabilización antropomorfa.

El ciclo representado en el círculo adquiere gran importancia en las culturas antiguas. La numeración basada en doceavos generaría a su vez un primer sistema de numeración, que ahora conocemos como el SISTEMA SEXAGESIMAL.
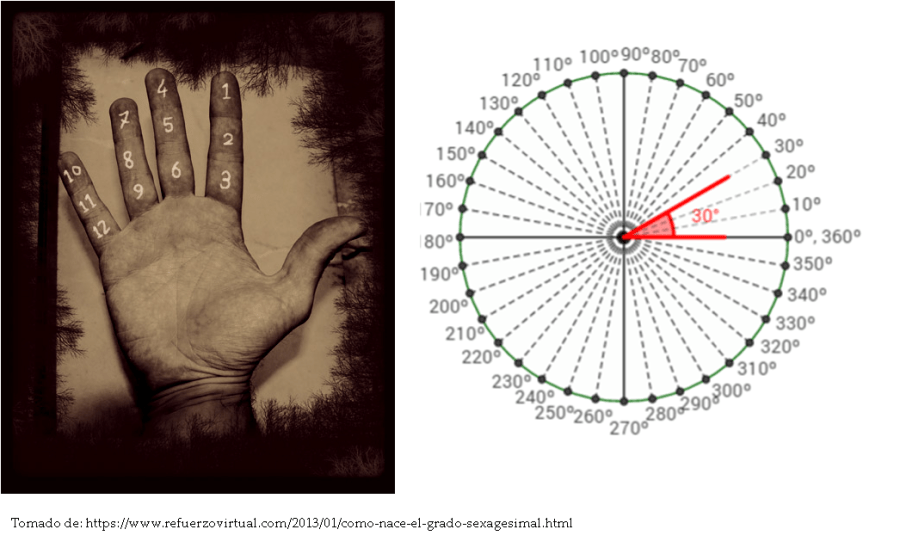
LA ESCRITURA Y EL ÁLGEBRA
El paralelo entre la escritura y la numeración propicia el desarrollo de las matemáticas.

Esta primer expresión de escritura se encuentra en el poema de Gilgamesh, que hace parte de la cultura MESOPOTÁMICA de BABILONIA.
“Aquel que vio todo hasta los confines de la tierra, Que todas las cosas experimentó, consideró todo. […] juntamente […], […] de sabiduría, que todas las cosas.[..]. (5) Lo oculto vio, desveló lo velado. Informó antes del Diluvio, Llevó a cabo un largo viaje, cansado y derrengado. Todo su afán grabó en una estela de piedra. De la terraplenada Uruk el muro construyó, Del reverenciado Eannal, el santuario puro. “
Epopeya de Gilgamesh , tablilla I . (612 a.c.)
En escritura CUNEIFORME así se expresaban los primeros números:

Como se observa en la figura el 60 es el número clave de este sistema de numeración que llamaremos SEXAGESIMAL, este sistema se emplea en la medición del espacio circular en grados:

Mediante este sistema se realizan variedad de operaciones matemáticas y transformaciones de mediciones.
LOS PROBLEMAS Y EL ÁLGEBRA
Son muchas las situaciones en las cuales la matemáticas sería la solución a problemas cotidianos que se presentaban en estas primeras civilizaciones.
El primer problema escrito del que tenemos referencia se encuentra en un PAPIRO EGIPCIO:

ESte primer planteamiento nos muestra que las ecuaciones ya se empezaban a emplear par modelar las situaciones o problemas de la cotidianidad.
MATEMÁTICAS EN OTRAS CULTURAS
A pesar que es en BABILONIA y EGIPTO donde se encuentran los orígenes escritos de las matemáticas, otras culturas también exploraron el álgebra:
EN LA CULTURA CHINA

EN LA CULTURA HINDÚ:

EN LA CULTURA GRIEGA:


Y EN LA CULTURA ÁRABE LA PRIMERA APARICIÓN DE UN LIBRO DE ALGEBRA:

TEXTO Y CONTEXTO EN MATEMÁTICAS
Las matemáticas y todas las ramas que conocerás en tu paso por el bachillerato (aritmética, álgebra, trigonometría, cálculo, análisis de funciones, geometría, estadística y probabilidades) parten de la realidad. Por muy abstractas que te parezcan tienen su origen en las situaciones cotidianas que la humanidad a vivido…que tu vives a diario.
Si no existe una situación problema o necesidad real de donde partir…no existiría la posibilidad de hacer un desarrollo matemático. Por eso cada cosa que sucede ( el vuelo de un ave, el viento, tu caminar y tu respiración, etc) puede volverse matemáticas.
Para iniciarnos en este mundo de percepción matemáticas partiremos con el TEXTO ESCRITO como elemento para reconocer un proceso científico y aprender a mirar con los lentes de las matemáticas.
EJERCICIO DE LECTURA
Veamos este texto sacado del Antiguo Testamento, Génesis 5:27:
Era Matusalén de 187 años cuando engendró a Lamec; vivió 782 años, y engendró hijos e hijas. Fueron todos los días de Matusalén 969, y murió. Era Lamec de 182 años cuando engendró un hijo, al que puso el nombre de Noé (…). Vivió Lamec, después de engendrar a Noé, 595 años, y engendró hijos e hijas. Fueron todos los días de Lamec 777 años, y murió (…). A los 600 años de la vida de Noé, el segundo mes, el día 17 de él, se rompieron todas las fuentes del abismo, se abrieron las cataratas del cielo, y estuvo lloviendo sobre la tierra durante 40 días y 40 noches.
TU SUBRAYAS Y SACAS LAS IDEAS Y CONCEPTOS PRINCIPALES.
EL CONTEXTO SOCIAL
Aquí te doy algunas ideas:
EL ANTIGUO TESTAMENTO
Sabes algo de los rollos del mar muerto?¿Qué elemento matemático podrías obtener de esta imagen?

Tomado de: https://www.tes.com/lessons/S8QL2a2N28v5fg/copy-of-primary-sources-their-place-in-the-classroom
MATUSALEN, LAMEC Y NOE
Son solo algunos de los personajes que integran una GENEALOGÍA.

Tomado de: http://davidnesher.com.ar/una-genealogia-con-codigos-de-esperanza-mesianica/
Igualmente de la anterior imagen: ¿Qué información matemática nos trae la imagen?
EL DILUVIO UNIVERSAL: SE ABRIERON LAS CATARATAS DEL CIELO, SE ROMPIERON TODAS LAS FUENTES DE ABISMO..
La siguiente gráfica nos indica como posiblemente se fue inundando la tierra para esa fecha del diluvio:

Tomado de: https://www.vix.com/es/btg/curiosidades/9159/2-teorias-cientificas-que-explican-el-mito-del-diluvio-universal
¿Que información matemática podemos extraer de la anterior gráfica?
EL CONTEXTO MATEMÁTICO
Este problema a diferencia del anterior contiene un CONTEXTO MATEMÁTICO cuyo objetivo según lo leíste ( habla de tres personajes y de edades) es:
- Fijar una cronología en la vida de Matusalén:
- MATUSALÉN (M) murió a los 969 años
- cuando MATUSALEN (M) tenía 187 años engendró a su hijo LAMEC ( L)
- al cumplir LAMEC ( L) 182 años engendró a su hijo NOE (N)
- por último, se produjo el Diluvio cuando NOE (N) tenía 600 años.
Si te diste cuenta entre paréntesis coloque la letra inicial de cada nombre, para simplificarlo,,, en otras palabras los convertí en VARIABLES.
La siguiente imagen actúa como soporte reducido de la información antes esquematizada y permite plantear un problema y, a la vez, intuir de qué tipo es y conjeturar su solución:

- Conocimiento esquemático:
- En este caso, es un simple problema aritmético y se resuelve con una suma:
- Cada letra representa un espacio de tiempo en años:
M + L + N = Tiempo entre el nacimiento de MATUSALÉN y el DILUVIO
Desde que que nació MATUSALÉN hasta el día del diluvio Universal pasaron entonces:
187 años + 182 años + 600 años = 969 años
Podemos afirmar que MATUSALÉN murió el mismo año que ocurre el diluvio universal.
Como pudiste observar en el desarrollo del texto hicimos un recorrido por toda la información que el texto nos puede dar y además tratamos de ver que elementos de matemáticas podíamos encontrar. Esa es una buena estrategia de trabajo en todas tus lecturas.
NOTA: TEN PRESENTE EL SÍMBOLO DE IGUALDAD ¿TIENE EL SIGNIFICADO DE EQUIVALENCIA?
LAS ECUACIONES Y EL ÁLGEBRA
No existe nada en matemáticas que no parta de una necesidad, una situación o un problema.
Cuál es la distancia entre Mosquera y la Mesa?
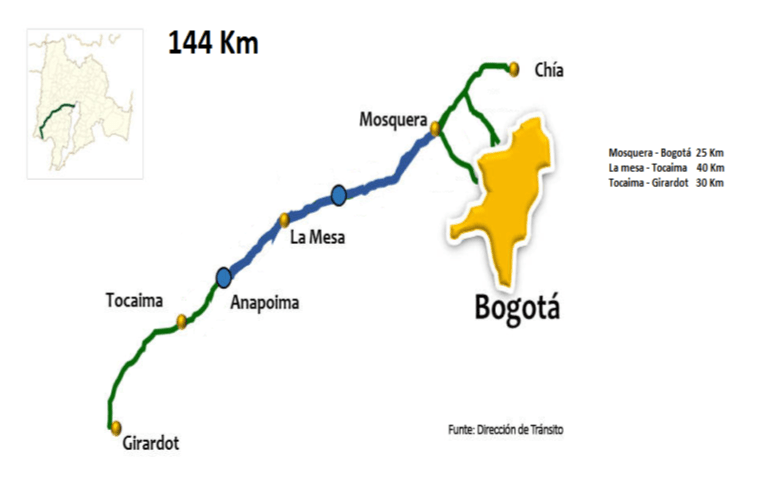
Al tener un problema matemático lo primero que tenemos que hacer es buscar datos, que en el caso anterior aparecen en una gráfica (mapa). En la gráfica nos indican la distancia total entre BOGOTÁ-GIRARDOT que es de 144 Km, y también nos indican las distancias entre algunas ciudades intermedias de tal manera que para llegar de BOGOTÁ A GIRARDOT la secuencia a seguir sería:
BOGOTÁ-MOSQUERA + MOSQUERA-LA MESA + LA MESA-TOCAIMA + TOCAIMA-GIRARDOT = 144 KM.
Si reemplazamos por valores numéricos en Kilómetros cada distancia de acuerdo a los datos que tenemos nos quedaría la siguiente ECUACIÓN:
25+X+40+30=144
Donde la X representa la incógnita o valor a encontrar en nuestro problema. La solución es sencilla, X= 49 Km. Esta sería la distancia entre MOSQUERA- LA MESA.
CARACTERÍSTICAS DE UNA ECUACIÓN
De la ecuación anterior podemos deducir:

CLASIFICACIÓN DE LAS ECUACIONES ALGEBRAICAS
El siguiente mapa resume los elementos característicos de una ecuación que nos permite clasificarlas, en el algebra de Baldor ( pag. 5 – 19) podrás profundizar en cada elemento:
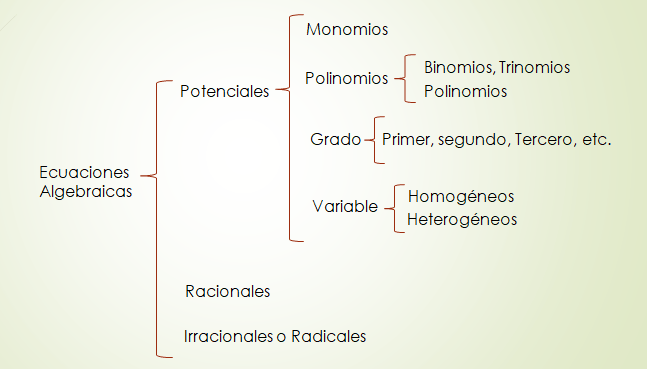
Lo anterior implica que el mundo de la numeración es bastante amplio y debemos recordar y reconocer:
EL MUNDO NUMÉRICO
La siguiente gráfica nos trae el recuerdo de la clasificación de los números. ¿Podemos hacer analogía con la clasificación de las ecuaciones algebraicas?
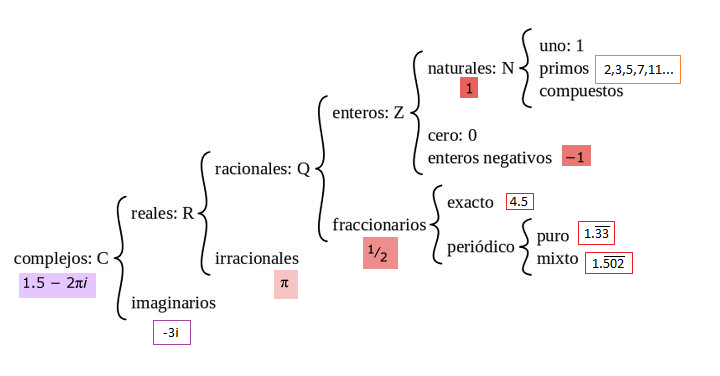
OPERACIONES CON ECUACIONES
Todas las ecuaciones parten de textos y contextos reales. Una vez llevadas al lenguaje matemático nos facilita la operatividad con ellas, veamos las principales operaciones matemáticas que podemos realizar con ellas:
SUSTITUCIÓN Y VALOR REAL
Es el proceso mediante el cual sustituyo una variable por un valor numérico y realizo las operaciones correspondientes para hallar el valor real de la ecuación.
ejemplo:
ENUNCIADO
Compré tres cajas de lápices y dos de marcadores. Si cada caja de lápices tiene un costo de $50 y cada caja de marcadores $80. ¿Cuál es el costo total de la compra?
VARIABLES:
L= lápices M= marcadores
DATOS:
L= $50 M=$80
ECUACIONES:
3L + 2M = Costo Total
PROCEDIMIENTO:
3($50) + 2($80) = $150 + $160 = $310
RESPUESTA:
El costo total de la compra es de $310
REDUCCIÓN
Es la operación que permite realizar simplificar términos algebraicos en los polinomios que se suman o restan. La reducción sólo funciona cuando los términos son semejantes, es decir que tienen las mismas variables en el mismo grado.
Para realizar una reducción adecuadamente debemos tener en cuenta las leyes de los signos:

En la reducción se agrupan los términos llamados semejantes ( tienen las mismas variables y con el mismo grado) y se suma o restan los valores numéricos de cada término.
CASO 1: TÉRMINOS SEMEJANTES DE IGUAL SIGNO
Ejemplo:
-8x – 4x – 2x – x – 3x
En este caso y siguiendo la ley de los signos para suma y resta simplemente «signos iguales se suman» y la respuesta «hereda» el mismo signo:
-8x – 4x – 2x – x – 3x = -18x
CASO 2: TÉRMINOS SEMEJANTES DE DIFERENTES SIGNOS
Ejemplo:
-8x + 4x + 2x – x + 3x
En este caso organizamos los términos, primero colocamos los de signo positivo y luego los de signo negativo:
+ 4x + 2x + 3x – 8x – x
Realizamos una reducción entre los términos de signo positivo: + 4x + 2x + 3x = +9x
Realizamos una reducción entre los términos de signo negativo: – 8x – x = -9x
Unimos ambos resultados y obtenemos la respuesta(según leyes de los signos):
+9x – 9x = 0
CASO 3: TÉRMINOS SEMEJANTES POR AGRUPACIÓN
ejemplo:
REDUCIR EL SIGUIENTE POLINOMIO
1 + x + xy – 2 + 2x -3xy -3 + 2xy – 3x
PRIMERO ORGANIZAMOS LOS TÉRMINOS POR SEMEJANZA: iniciamos por los términos con «x» y luego los términos con «xy» y finalizamos con los números ( se recomienda colocar primero todos los que tengan signo positivo y al final los que tengan signo negativo, debidamente agrupados):
(x + 2x – 3x) + (xy + 2xy – 3xy) + (1 – 2 – 3)
SEGUNDO REALIZAMOS LAS OPERACIONES DE SUMA O RESTA SEGÚN LOS TÉRMINOS:
(0) + (0) + (-4) = -4
RESPUESTA:
1 + x + xy – 2 + 2x -3xy -3 + 2xy – 3x = -4
REDUCCIÓN Y PARÉNTESIS
En algunos casos antes de realizar la reducción debemos resolver paréntesis, aplicando las leyes de los signos y teniendo en cuenta el orden de los paréntesis:
{[()]}
Ejemplo:
REDUCIR EL SIGUIENTE POLINOMIO:
4 – (2a +3) + (4a +5) – (7 – 3a)
PRIMERO RESOLVEMOS LOS PARÉNTESIS:
4 – 2a – 3 + 4a + 5 – 7 +3a
SEGUNDO ORGANIZAMOS POR TÉRMINOS SEMEJANTES: (primero positivos, luego negativos)
(4a + 3a -2a) + (4 + 5 – 3 – 7)
TERCERO REALIZAMOS LAS OPERACIONES
5a – 1
RESPUESTA:
4 – (2a +3) + (4a +5) – (7 – 3a) = 5a – 1
EJERCICIOS SUGERIDOS:
Algebra de Baldor: EJERCICIO 7, EJERCICIO 9, EJERCICIO 10, EJERCICIO 12.
LAS OPERACIONES BÁSICAS
SUMA
La suma de las expresiones algebraicas (miembros de una ecuación) depende de las cualidades de los términos:
CASO 1: SUMA DE MONOMIOS CON TÉRMINOS NO SEMEJANTES
Ejemplo:
Sumar : m, – p, 2n
En este caso escribimos un término al lado del otro realizando la operación de suma indicada:
(m) + (- p) + (2n)
Observamos que no hay operaciones entre los paréntesis y aplicando las leyes de los signos para multiplicación resolvemos los paréntesis:
m – p + 2n
El resultado es un trinomio de primer grado sin términos semejantes.
CASO 2: SUMA DE MONOMIOS CON TÉRMINOS SEMEJANTES
Ejemplo:
Sumar: a, -3b, -8c, 4b, 2a
En este caso como en el anterior inicialmente unimos los términos para construir un polinomio:
a -3b -8c + 4b + 2a
Aplicamos el CASO 3 de reducción realizando la operación indicada de la suma y agrupando los términos ( primero los positivos y luego los negativos dentro del paréntesis):
(a + 2a) + (4b -3b) + (-8c)
Realizamos primero las operaciones dentro del paréntesis:
(3a) + (b) + (-8c)
Aplicando las leyes de los signos para multiplicación resolvemos los paréntesis :
3a + b -8c
Esta sería la respuesta.
CASO 3 SUMA DE POLINOMIOS
Ejemplo:
Sumar: – am + 6mn – 4s ; 6s – am – 5mn
Inicialmente unimos todos los términos en un polinomio mediante la operación de suma indicada:
(- am + 6mn – 4s) + (6s – am – 5mn)
Aplicando las leyes de los signos para multiplicación resolvemos los paréntesis y reagrupamos los términos por semejanzas ( primero los positivos y luego los negativos):
(- am – am) + (6 mn – 5mn) + (6s -4s )
Realizamos las operaciones dentro de los paréntesis:
(-2am) + (mn) + (2s)
Aplicando las leyes de la multiplicación de signos resolvemos los paréntesis:
-2am +mn +2s
Obtenemos como respuesta un trinomio de primer grado.
En el Algebra de Baldor encontrarás otra forma de hacerlo agrupando por columnas los polinomios.
EJERCICIOS SUGERIDOS:
Algebra de Baldor: EJERCICIO 16, EJERCICIO 17, EJERCICIO 18.
RESTA
El proceso es similar al anterior solo tenemos en cuenta la ley de los signos en multiplicación para resolver los paréntesis.
CASO 1: RESTA DE MONOMIOS CON TÉRMINOS NO SEMEJANTES
Ejemplo:
Restar : – m de – p
En este caso escribimos un término al lado del otro realizando la operación de resta indicada:
(- p) – (-m)
Observamos que no hay operaciones entre los paréntesis y aplicando las leyes de los signos para multiplicación resolvemos los paréntesis:
-p + m
El resultado es un binomio de primer grado sin términos semejantes.
CASO 2: RESTA DE MONOMIOS CON TÉRMINOS SEMEJANTES
Ejemplo:
Restar: -3b de – 4b
En este caso escribimos un término al lado del otro realizando la operación de resta indicada:
(-4b) – (-3b)
Resolvemos los paréntesis y realizamos la reducción:
-4b + 3b = -b
Esta sería la respuesta.
CASO 3 RESTA DE POLINOMIOS
Ejemplo:
Restar: – am + 6mn – 4s de 6s – am – 5mn
Inicialmente unimos todos los términos en un polinomio mediante la operación de resta indicada:
(6s – am – 5mn) – (- am + 6mn – 4s)
Aplicando las leyes de los signos para multiplicación resolvemos los paréntesis:
6s – am – 5mn + am – 6mn +4s
y reagrupamos los términos por semejanzas ( primero los positivos y luego los negativos):
(- am + am) + (- 6 mn – 5mn) + (6s + 4s )
Realizamos las operaciones dentro de los paréntesis:
(0) + (-11mn) + (10s)
Aplicando las leyes de la multiplicación de signos resolvemos los paréntesis:
-11mn +10s
Obtenemos como respuesta un binomio de primer grado.
En el Algebra de Baldor encontrarás otra forma de hacerlo agrupando por columnas los polinomios.
EJERCICIOS SUGERIDOS:
Algebra de Baldor: EJERCICIO 22, EJERCICIO 24.
MULTIPLICACIÓN
El proceso de multiplicación se rige por las leyes de los signos y por las leyes de la potenciación en caso de las variables.
Recordemos las leyes de la potenciación:

CASO 1: MULTIPLICACIÓN ENTRE MONOMIOS
Ejemplo:
Hallar el producto de: – 4xn por 5n
Indicamos la operación:
(- 4xn)(5n)
Se multiplican inicialmente los signos (-) del término 4nx y (+) del término 5n según las leyes de los signos. Luego se multiplican los números (4) y (5) correspondiente a cada término. Por último las letras que sean semejantes según las leyes de la potenciación, en nuestro caso la n por la n al tener exponente=1 se suman los exponentes y nos da una letra n elevada al cuadrado:
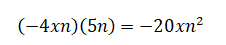
Como observamos la letra x al no tener con quien operar queda igual.
CASO 2: MULTIPLICACIÓN ENTRE MONOMIO Y POLINOMIO
Ejemplo:
Hallar el producto entre:

En este caso el primer monomio se encarga de multiplicar a cada término del binomio, uno a uno, primero los signos, luego los números y finaliza con las letras semejantes, aplicando las leyes de los signos y de la potenciación:

Al finalizar obtenemos como resultado:
![]()
CASO 3: MULTIPLICACIÓN ENTRE POLINOMIOS
Como en el caso anterior cada término de un polinomio multiplica a cada término del otro polinomio, uno a uno empleando la misma regla: signo por signo (con la ley de los signos), número por número y letra semejante por letra semejante (con la ley de la potenciación):
Ejemplo:

En este caso se multiplica el primer término del primer polinomio por el primer término del segundo y luego por el segundo término del segundo polinomio. La operación uno a uno se repite para cada término:

Al final tenemos un polinomio de 4 términos para este caso:

EJERCICIOS SUGERIDOS:
Algebra de Baldor: EJERCICIO 40, EJERCICIO 42 y EJERCICIO 44.
DIVISIÓN
La división como su nombre lo indica nos invita a separar en partes una expresión algebraica. Igual a la multiplicación se trabaja término a término (uno por uno), inicialmente los signos bajo la ley de los signos, luego los números que se pueden simplificar y por último las letras semejantes de acuerdo a las leyes de la potenciación.
CASO 1: DIVISIÓN DE MONOMIOS
Como se dijo anteriormente se opera elemento por elemento del término:
Dividir:
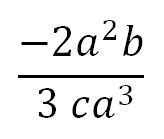
En este caso según la ley de los signos (-) / (+) nos da como resultado una fracción negativa. Los números no se pueden seguir simplificando pues se transformarán en decimales. La letra (b) del numerador no tiene en el denominador una letra semejante par operar, al igual que la letra (c) por lo tanto quedan igual. Solo la letra (a) puede operarse por las leyes de la potenciación, es decir se restan sus exponentes:
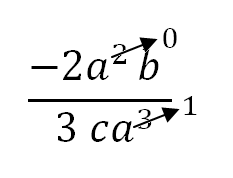
En el numerador (a) elevada a la cero (0) es uno (1), y en el denominador al quitarle (2) al exponente (3) de la letra (a) queda elevada a la uno (1):
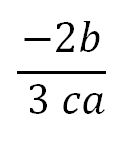
CASO 2: DIVISIÓN DE UN POLINOMIO POR UN MONOMIO
En este caso solo se separa cada polinomio en el mismo monomio y se realiza el procedimiento anterior:
Dividir:

Separamos cada elemento:

Aplicando las leyes de la potenciación eliminamos exponentes:

Dividimos los números correspondientes: En el primer término (3)/(3) = 1, en el segundo término (6)/(3) = 2 y en el tercer término (9)/(3)= 3. Nos queda al final:

CASO 3: DIVISIÓN DE POLINOMIO POR POLINOMIO
Esta división tiene siempre en cuenta aquel valor o expresión algebraica que pueda anular un término del polinomio llamado DIVIDENDO, al multiplicarse por el término llamado DIVISOR. Inicialmente debemos observar que las expresiones están organizadas según los exponentes en orden descendente con relación a una letra.
DIVIDIR:

Lo expresamos de la siguiente manera:

Buscamos el término que multiplicado por (x) del divisor me dé como resultado 3x al cuadrado: (3x)

Multiplicamos este valor por cada término del divisor y se lo restamos (cambiamos signos) al dividendo:

Cada resultado obtenido de la multiplicación se coloca en la respectiva columna, se realiza la operación y se baja el siguiente término:
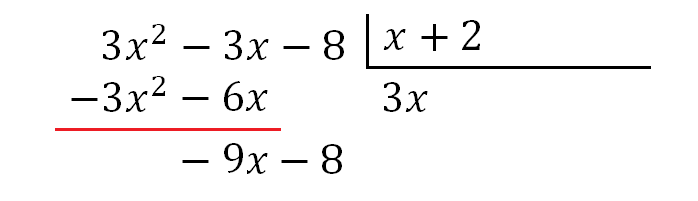
Volvemos a buscar el número que multiplicado por (x) del divisor nos dé como resultado (-9x) del Dividendo, en este caso sería -9. Realizamos las operaciones indicadas:

Entonces el resultado de nuestra división es:
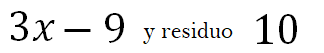
Nuestra división no es exacta.
EJERCICIOS SUGERIDOS:
Algebra de Baldor: EJERCICIO 53, EJERCICIO 54
NOTA: INDAGA OTROS MÉTODOS DE REALIZAR LA DIVISIÓN.
NOTA: RECUERDA ESTAR AL DÍA CON TUS TRABAJOS EL PRIMER CORTE DE NOTAS SE REALIZA EL 10 DE AGOSTO DE 2018.
Simplificando las ecuaciones
FACTORIZACION
Esta es la principal operación de este curso, nos permite representar mediante un producto de dos expresiones algebraicas un polinomio.
Recuerdas cuando realizamos la multiplicación de expresiones algebraicas? en el ejemplo:

nos daba como resultado:

en la factorización partiremos del resultado para hallar los productos, es decir es un proceso REVERSIBLE.
entonces dependiendo del polinomio al cual nos enfrentemos hay DIEZ formas o casos a partir del cual podemos trabajar el polinomio hasta convertirlo en el producto de dos o más expresiones algebraicas.
CASO 1: FACTOR COMÚN
CONDICIONES:
- Puede tener cualquier cantidad de términos
- Debe tener un elemento común ( número o letra) entre todos sus elementos.
- Siempre se factoriza el MÚLTIPLO MÍNIMO COMÚN o la letra CON MENOR EXPONENTE
Existen dos posibilidades:
PRIMERA: CUANDO EL ELEMENTO COMÚN ES UN MONOMIO
En el ejemplo tenemos un trinomio que tiene dos elementos comunes: los números son múltiplos entre sí y además los tres términos tienen la letra x en común. Es un caso 1: FACTOR COMÚN!
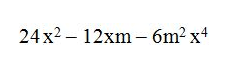
De los números múltiplos es el 6 el mínimo a multiplicar y por tanto a factorizar, lo sacamos del polinomio y generamos un paréntesis de tal forma que si volviésemos a multiplicar por el 6 obtendremos los mismos números que el polinomio inicial:
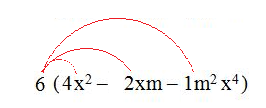
Ahora extraemos la letra común (x) con su menor exponente es decir uno (1):

Al realizar las operaciones entre las potencias obtenemos:
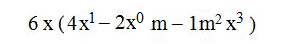
Pero como un exponente de grado uno no se escribe y un exponente de grado cero es igual a la unidad, entonces:
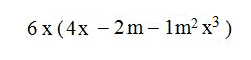
Esta sería nuestra respuesta:

SEGUNDA: CUANDO EL ELEMENTO COMÚN ES UN POLINOMIO
En el ejemplo tenemos un binomio cuyo elemento común se encuentra entre paréntesis (resaltado en amarillo, al extraerse del binomio deja dos elementos ( 2x , y) que se encierran en un nuevo paréntesis con sus respectivos signos:

EJERCICIOS SUGERIDOS:
Algebra de Baldor ejercicios 89 y 90.
CASO 2: FACTOR COMÚN POR AGRUPACIÓN
CONDICIONES:
- Solo se emplea para polinomios cuya cantidad de términos sea par.
- Se deben agrupar (organizar) los términos de tal forma que podamos tener en cada par o trío de términos elementos comunes que al ser extraídos generen un nuevo elemento común ( como en el caso 1 en su segunda forma).
En el siguiente ejemplo agruparemos el mismo polinomio de dos formas diferentes teniendo en cuenta los elementos comunes, al final el resultado es el mismo:

al final si hemos sabido agrupar bien los términos obtendremos el mismo resultado.
EJERCICIOS SUGERIDOS:
Algebra de baldor, ejercicio 91
CASO 3: TRINOMIO CUADRADO PERFECTO
CONDICIONES:
- Debe tener tres términos
- El primero y el último de sus términos debe estar elevado al cuadrado o a una potencia par.
- Al extraer las raíces del primer y tercer término y multiplicarlas por dos (2) nos debe dar como resultado el segundo término: es perfecto!
Aunque parece un poco complicado cumplir con estas condiciones, el simple hecho de verificarlas nos ayuda con el proceso de solución del caso.
Veamos el ejemplo:
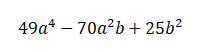
Verifiquemos que cumple con las condiciones:
- Tiene tres términos ( OK)
- Se le puede sacar raíz cuadrada al primer y al tercer término? (OK)

3. Al multiplicar estos dos resultados por dos (2) Obtenemos el término de la mitad? (OK es perfecto!)

Cumple con las condiciones. Entonce elaboramos la respuesta así:
- Tomamos los resultados de las raíces y los unimos formando un binomio cuyo signo entre ellos es el signo que acompaña al segundo término del trinomio (-).
- Encerramos entre paréntesis este binomio y lo elevamos al cuadrado, obtenemos así un producto notable que es la respuesta:

EJERCICIO SUGERIDO:
Algebra de Baldor, ejercicio 92
CASO 4: DIFERENCIA DE CUADRADOS PERFECTOS
CONDICIONES:
- Debe tener solo dos términos
- Los dos términos deben estar unidos mediante una RESTA, signo menos(-).
- Los dos términos deben estar al cuadrado o a una potencia par, pues se les debe poder sacar raíz cuadrada.
Veamos el ejemplo:
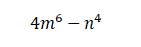
Verificamos que cumple las condiciones:
- Tiene dos términos (OK)
- En medio de los dos términos hay un signo menos? (OK)
- A ambos términos se les puede sacar raíz cuadrada? (OK)
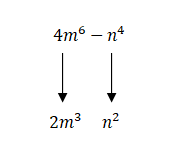
4. Entonces al cumplir con las condiciones se puede construir la respuesta. Tomamos los resultados de las raíces cuadradas y construimos dos binomios, uno de ellos sumando los dos resultados y otro restando los mismos resultados, encerramos entre paréntesis cada binomio y los multiplicamos, obtenemos así la respuesta:
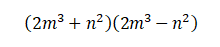
EJERCICIO SUGERIDO:
Algebra de Baldor, ejercicio 93 y 94.
CASO 5: TRINOMIO CUADRADO PERFECTO POR ADICIÓN Y SUSTRACCIÓN
CONDICIONES:
- Debe tener tres términos
- El primer y el tercer término tienen raíz cuadrada.
- Al multiplicar la raíz cuadrada del primer y el tercer término NO se obtiene el término de la mitad, es decir NO ES TRINOMIO CUADRADO PERFECTO.
Veamos el ejemplo:

Se comprueba que no es un trinomio cuadrado perfecto, que le hace falta sumar 1a∧2 y se obtiene el 2a∧2 requerido. Pero para que no altere la ecuación debemos también restar dicho valor:

Se obtiene al final un caso 4 de factorización cuya respuesta es:

EJERCICIO SUGERIDO:
Ejercicio 96 del álgebra de Baldor.
CASO 6: TRINOMIO CUADRADO DE LA FORMA
CONDICIONES:
- Tiene tres términos
- El primer término tiene un 1 que acompaña a una letra cualquiera; pero a esta letra se le puede sacar raíz cuadrada.
- El segundo término tiene la misma letra que el primer término pero con potencia 1.
- El tercer término no tiene letra, es solo un número.
Ejemplo:

Se le saca la raíz al primer término y se construyen dos paréntesis:
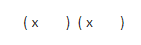
En el primer paréntesis se coloca el signo del segundo término y en el segundo paréntesis el resultado de multiplicar el signo del segundo término por el signo del tercer término.

Ahora buscamos dos números que multiplicados nos de el tercer término (10) y sumados ( porque los dos signos de los paréntesis son iguales) nos de el número que acompaña al segundo término (7). Esos números son 5 y 2:

EJERCICIO SUGERIDO:
Ejercicios sugeridos 98 y 99 del álgebra de Baldor.
CASO 7: TRINOMIO CUADRADO DE LA FORMA

CONDICIONES:
- Tiene tres términos.
- El primer término tiene un número diferente del 1 que acompaña a una letra, a esta letra se le puede sacar raíz cuadrada.
- El segundo término tiene la misma letra que el primer término pero con potencia 1.
- El tercer término no tiene letra, es un número cualquiera.
ejemplo:
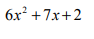
Se toma el número que acompaña al primer término (6) y lo multiplicamos por los tres términos:
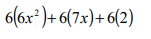
En el primer término elevamos al cuadrado, en el segundo término intercambiamos los números y en el tercer término realizamos la multiplicación:

Ahora hemos transformado el caso 7 en caso 6. Buscamos dos números que multiplicados nos den 12 pero que sumados nos den 7…estos números son : 4 y 3 .
Pero así como multiplicamos por (6) debemos dividir por (6) para que no se altere la ecuación. Sin embargo 6 = (2) (3)
Dividimos el primer paréntesis por dos y el segundo por tres para obtener la respuesta:

EJERCICIO SUGERIDO:
ejercicios 100 y 101 del álgebra de Baldor.
CASO 8: CUBO PERFECTO DE BINOMIOS
CONDICIONES:
- Tiene cuatro términos.
- Al primer y al cuarto término se le puede sacar raíz cúbica.
- El triple producto del cuadrado de la raíz del primer término por la raíz de cuarto término da como resultado el segundo término.
- El triple producto de la raíz del primer término por el cuadrado de la raíz del cuarto término da como resultado el tercer término.
como ejemplo:
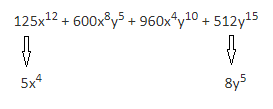
Luego de sacar las raíces cúbicas del primer y el cuarto término comprobamos:
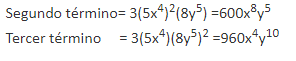
Al comprobar lo anterior construimos la respuesta, tomamos las dos raíces cúbicas colocamos el signo que acompaña al segundo término y elevamos al cubo:

EJERCICIO SUGERIDO:
Ejercicio 102 del álgebra de Baldor
CASO 9: SUMA O DIFERENCIA DE CUBOS PERFECTOS:
CONDICIONES:
- Tiene dos términos.
- Los dos términos pueden estar unidos mediante una suma o una resta.
- A los dos términos se les puede sacar raíz cúbica.
- La respuesta depende de las ecuaciones:

Ejemplo:

Luego de sacar las raíces cúbicas construimos la respuesta según las ecuaciones anteriores:
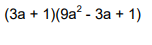
EJERCICIO SUGERIDO:
Ejercicio 103 Algebra de Baldor.
CASO 10: SUMA O DIFERENCIA DE DOS POTENCIAS IGUALES
CONDICIONES:
- Tiene dos términos
- Los dos términos pueden estar unidos mediante una resta o una suma.
- No se les puede sacar ni raíz cuadrada, ni raíz cúbica.
- Se resuelve mediante una división entre los términos que se obtienen luego de sacar las raíces correspondientes a la potencia indicada.
Ejemplo:
Luego de sacar la raíz quinta de los dos términos realizamos la división:

La respuesta de este caso es:
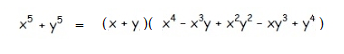
EJERCICIO SUGERIDO:
Ejercicio 105 Álgebra de Baldor.
TALLERES PROPUESTOS
Los siguientes son los talleres propuestos en clases:
TALLER SUSTITUCION SEXAGESIMAL Y TEXTOS EN ECUACIONES
TALLER DE REDUCCION Y SUSTITUCION
TALLER DE SUSTITUCIÓN SUMA Y RESTA COMBINADAS
TALLER MULTIPLICACION Y DIVISION
TALLER FACTORIZACION CASO 1 Y 2
TALLER FACTORIZACION CASO 3 Y 4
TALLER FACTORIZACION CASOS 7 Y 8
GEOMETRÍA Y FACTORIZACIÓN
Visualizar los casos de factorización es una necesidad por cuanto debemos llevar al plano gráfico la abstracción de las matemáticas. Pero iniciemos con los conceptos mas simples de la geometría y así lo iremos comprendiendo.
PERÍMETRO
La suma de todos los lados de una figura geométrica es el concepto de perímetro:

De igual forma en lugar de datos numéricos podemos tener datos algebraicos:

ÁREAS Y FACTORIZACIÓN
Reconociendo las ecuaciones para el cálculo de una área básica:

Podemos calcular un área compuesta básica:
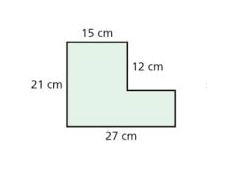
En la figura anterior faltan algunos datos, pero usando la lógica los podemos complementar:
21cm -12 cm= 9cm
27cm – 15cm = 12 cm
La figura tendría todos sus datos así:

Para hallar el área total la vamos a dividir en dos áreas:

De tal forma que:
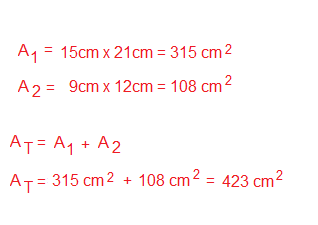
El mismo cálculo lo podemos realizar con expresiones algebraicas:

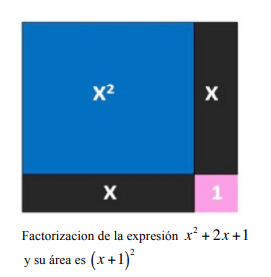
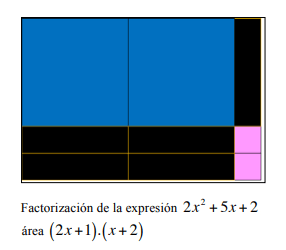
Uniendo las áreas anteriores obtenemos un área compuesta que es un caso de factorización, en este caso el caso 6:

Tomando el trabajo de la Guía didáctica para el aprendizaje de la factorización en estudiantes del CLEI IV del ITM cuya autora es Martha Eugenia Ospina Sepúlveda:
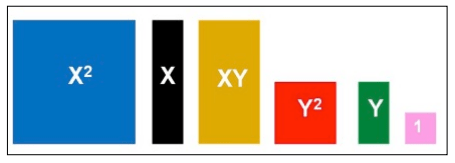
Podemos construir diferentes casos de factorización:
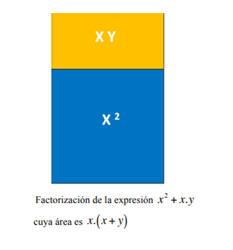
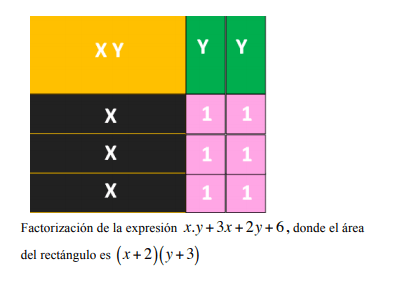

LA TERCERA DIMENSIÓN : VOLUMEN
Las tres dimensiones, es la expresión que involucra el conocimiento de los objetos con volumen, para los cuales existen ya fórmulas para su cálculo:
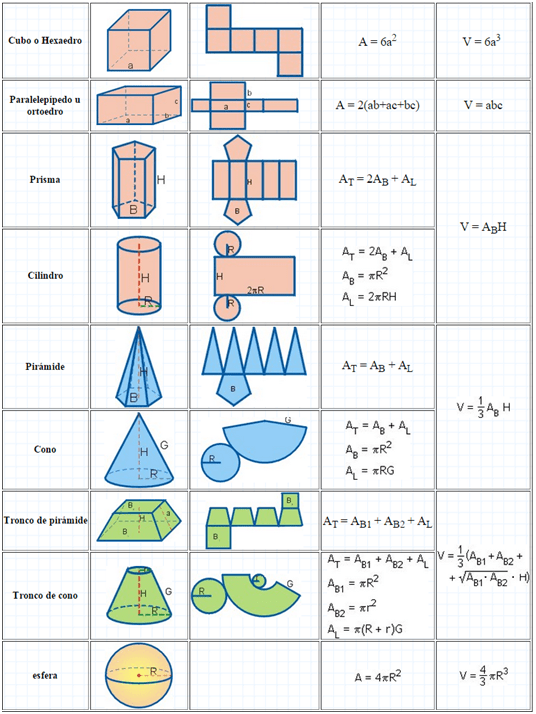
Tomado de: https://mauriciomedinasierra.wordpress.com/primer-corte/conceptos/volumen/tabla-de-areas-y-volumenes-figuras-geometricas/
También se puede consultar: http://blogdecarina.blogspot.com.co/2014/02/volumen-cuerpos-geometricos.html
En la tabla anterior se observa además del nombre y la forma de la figura tridimensional, el desarrollo del sólido correspondiente para su elaboración a partir de una superficie plana. Existe una columna donde aparece el cálculo del área superficial de cada figura y la ecuación del cálculo del volumen.
Gracias a estos valores podemos hacer cálculos con expresiones matemáticas:
EJEMPLO 1
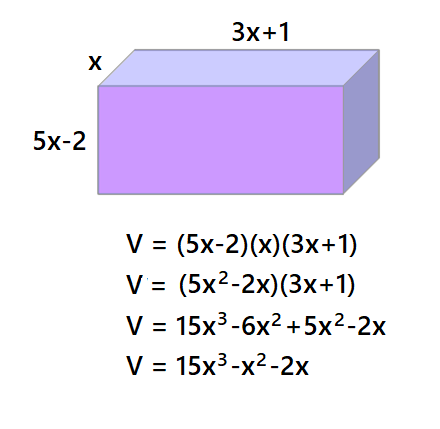
Tomado de: http://cremc.ponce.inter.edu/algebrageometrica/taller1.htm
EJEMPLO 2
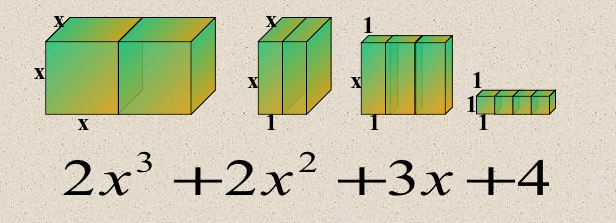
Tomado de: https://es.slideshare.net/MATEMATICASEEMM/polinomios-2700548
EJERCICIO
Calcular el volumen y simplificar la expresión algebraica.

Tomado de: http://ww2.educarchile.cl/PORTAL.HERRAMIENTAS/SIMCE2006/Ejercicios/Diagnostica_Segundo.aspx?sector=2&nivel=2&id_Eje=98
REPRESENTACIÓN VOLUMETRICA MEDIANTE PERSPECTIVA
Existen muchas formas de representar mediante el empleo del DIBUJO TÉCNICO una figura de volumen. Hagamos un alto y observemos este desarrollo de la geometría en el ARTE. Consideraremos solo tres formas de representación:
PERSPECTIVA CABALLERA
Esta forma de representación maneja una de las caras del objeto a 45 grados.
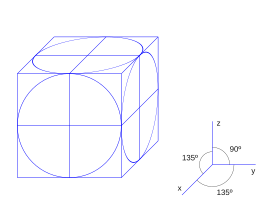
Tomado de: https://es.wikipedia.org/wiki/Perspectiva_caballera
PERSPECTIVA ISOMÉTRICA
Esta se caracteriza por representar un objeto en posición angular de 120 grados entre sus ejes, es la que usaremos en clases.

Tomado de: https://es.wikipedia.org/wiki/Proyecci%C3%B3n_isom%C3%A9trica
TALLER DE MODELOS ISOMÉTRICOS
Realizar el siguiente taller: Obteniendo las tres vistas principales de cada uno de los modelos isométricos. No es necesario elaborar las figuras. Puedes hacer hasta cuatro soluciones por hoja de papel milimetrado. Dale click al enlace siguiente, descarga e imprime el taller. Lo resuelves en hojas de papel milimetrado:
taller modelos isométricos recuperación
REPRESENTACIONES ISOMÉTRICAS PARA TRABAJAR EL CONCEPTO DE VOLUMEN:

Al calcular el volumen de estas figuras debes partir del volumen de un cubo (cada cuadrícula simboliza un centímetro) e ir restando elementos (paralelepípedos, prismas, cubos, etc) hasta obtener las figuras anteriores, tal como se explicó en clases.
EL TEOREMA DE PITÁGORAS
Aplicar este teorema es sencillo, la historia de pitágoras y sus seguidores la contaremos en clases. el teorema relaciona los tres lados de un triángulo llamado rectángulo que hace parte de los triángulos que tienen un ángulo de 90 grados:

con un ejemplo sencillo veremos como se aplica el teorema. Imagina que a ese niño se le enredó su cometa a 50 metros de distancia, en un poste de 6 m de altura. El quiere saber cuánto hilo hay desde su posición hasta la altura del poste…para ello emplea el teorema de pitágoras:

Ahora tú realiza el siguiente caso, vamos… a ver como te va!

Te dejo una curiosidad…¿Sabías que de esta manera un personaje calculó la altura de las pirámides de Egipto?
TALES DE MILETOS Y SU TEOREMA
El personaje del cual te hablaba es TALES DE MILETOS, investiga su biografía. Este es su teorema:

gracias a este teorema podemos conocer los lados de un triángulo mediante un concepto llamado semejanza de triángulos. Como puedes ver en la figura anterior hay dos triángulos rectángulos uno dentro de otro, el más pequeño lo forman los lados a y b; mientra que el grande lo forman los lados d y c. Simplemente por estar compartiendo el lado más largo (el rayo del sol) y el mismo ángulo, estos triángulos son semejantes.
Los criterios de semejanza y congruencia los estudiaremos en clases.
En fín…la ecuación que aparece entre los cuatro lados es el famoso teorema de Tales de Miletos y se puede usar en diversas formas:
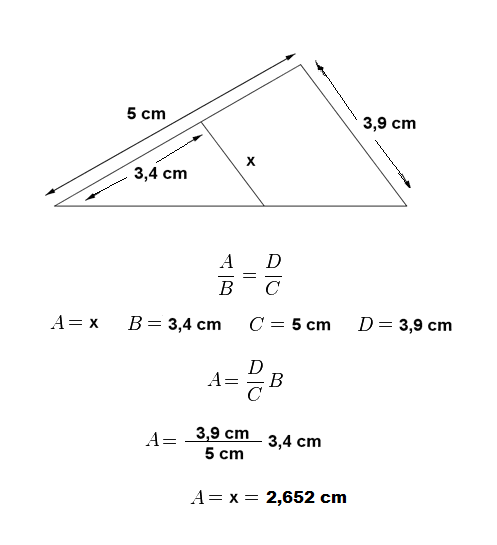
Ahora trata de hacer estos dos ejercicios:

GRÁFICAS EN PLANO CARTESIANO
Todas las ecuaciones del álgebra se pueden transformar en FUNCIONES para ser graficadas, solo basta en que se encuentre una variable en función de la otra, algo que se puede conseguir mediante el DESPEJE de una de ellas en la ecuación. En nuestro caso solo vamos a trabajar aquellas gráficas de dos variables lineales:
Supongamos que tenemos la ecuación del perímetro de un triángulo equilátero (todos sus lados son iguales):
P = 3L
Esta ecuación nos expresa que el perímetro (suma de los lados) en un triángulo equilátero es función de la longitud de sus lados. Es decir que si conozco el tamaño de uno de sus lados basta con multiplicar este valor por tres y obtendremos el valor del perímetro para este tipo de triángulo.
Basándose en lo anterior, puedo tomar diferentes valores para los lados de un triángulo equilátero , por ejemplo un triángulo de lado 1 cm, otro de 2 cm; etc. Los resultados los puedo expresar en una tabla como se observa en la figura.
Puedo graficar estos pares de puntos en un diagrama CARTESIANO (averigua porqué se llama así..) de tal forma:
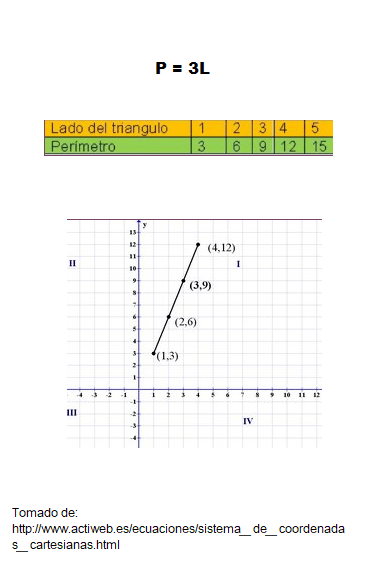
BASES INICIALES DE ESTADÍSTICA
Teniendo en cuenta que la Estadística nos permite RECOLECTAR, ORGANIZAR, PROCESAR, ANALIZAR e INTERPRETAR datos, esta es entonces una gran herramienta de trabajo para la matemáticas de la Física.
Algunos conceptos básicos a tener en cuenta son:
POBLACIÓN: Que es el conjunto total de los elementos a estudiar. (EJEMPLO: los 5230 estudiantes del Colegio)
MUESTRA: Es una parte de la Población que sea representativa de los datos recolectados. (650 estudiantes seleccionados 10 de cada salón)
VARIABLE: Es la característica a medir. Las variables pueden ser:
CUALITATIVAS: Cuando no se pueden medir numéricamente y a su vez pueden ser : NOMINALES: cuando sus valores no se pueden ordenar (EJEMPLO: Sexo, grupo sanguíneo, religión; etc). ORDINALES: cuando sus valores se pueden ordenar ( Poco, muy poco, satisfecho, nada satisfecho, intensidad, etc)
CUANTITATIVAS: Cuanto poseen un valor numérico, se pueden clasificar en: DISCRETAS: cuando solo pueden tomar un valor numérico entero (EJEMPLO: número de hijos). CONTINUAS: Cuando pueden tomar cualquier valor real (EJEMPLO: la altura de las personas)
AGRUPACIÓN DE DATOS
Para facilitar el trabajo con los datos se suelen agrupar en cuadros de FRECUENCIAS. En nuestro caso manejaremos DOS tipos de AGRUPACIÓN:
-
AGRUPACIÓN SIMPLE:
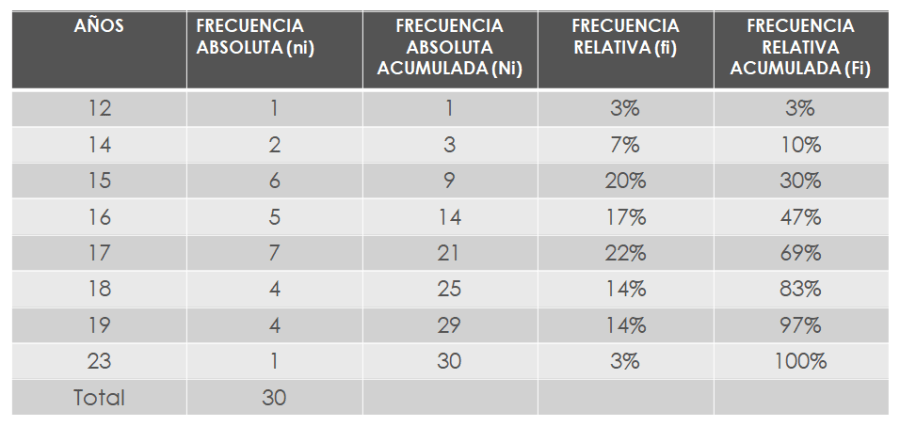
En este tipo de agrupación los datos se transcriben en orden ascendente directamente en la tabla de frecuencias, un dato por cada fila de la tabla.


Realiza el conteo de los datos..cuántos hay de cada uno en la tabla?
TIPOS DE FRECUENCIAS
Las frecuencias que emplearemos son:
FRECUENCIA ABSOLUTA:
Cantidad de veces que se repite el dato.
FRECUENCIA ABSOLUTA ACUMULADA:
Vamos sumando las frecuencias absolutas hasta llegar a la cantidad total de datos.
FRECUENCIA RELATIVA:
Cantidad porcentual del dato con respecto al total de datos. Se calculó tomando la frecuencia absoluta y dividiendola en el total de los datos. A ese resultado lo multiplicamos por cien y se obtiene en porcentaje.
FRECUENCIA RELATIVA ACUMULADA:
Así como hicimos con la frecuencia absoluta acumulado, hacemos con la frecuencia relativa, las vamos sumando de porcentaje en porcentaje hasta obtener el 100%.
Al final la tabla de datos AGRUPACIÓN SIMPLE queda de la siguiente forma:
FORMAS DE PRESENTACIÓN DE DATOS ESTADÍSTICOS
Para presentar de una forma visual y GRÁFICA los datos se emplean muchas formas de representación entre las cuales tenemos:
DIAGRAMA DE BARRAS
Recuerda que estas gráficas son como trabajar en un plano clartesiano.
EJEMPLO: para nuestra frecuencia absoluta datos agrupación simple.
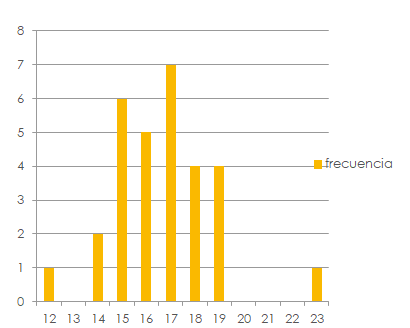
DIAGRAMA LINEAL o DE DISPERSIÓN
Estas gráficas son similares a realizar un trabajo en PLANO CARTESIANO:
EJEMPLO: para nuestra frecuencia absoluta datos agrupación simple.

ANÁLISIS DE DATOS ESTADÍSTICOS
Existen diversos estudios para el análisis estadístico de datos. Inicialmente veremos los ESTUDIOS DE MEDIDAS DE TENDENCIA CENTRAL:




RECUPERACIÓN FINAL GRADO OCTAVO
Si por alguna razón no alcanzaste los logros en esta asignatura debes realizar un trabajo de recuperación:
- Tu cuaderno en clases debe estar al día
- Debes presentar en una carpeta todos los talleres realizados
- Debes presentar nuevamente las evaluaciones que realizaste.
- Debes presentar las tareas que se dejaron completamente.
Una vez cumplas con los anteriores requisitos debes presentar una evaluación final y pasar dicha evaluación para haber recuperado los logros pendientes.
Gracias por haber estado en mi clase.
Este trabajo se realizará en este año el martes 6 de Noviembre de 2018 en la jornada tarde en las instalaciones del Colegio
Atte
JULIO ESTUPIÑAN
GRADO NOVENO
Bienvenidos estudiantes, con el fin de fundamentar elementos de matemáticas necesarios para el desarrollo de la FÍSICA 1 y 2, estas BASES apoyadas en los derechos básicos de aprendizaje para GRADO NOVENO nos pueden ser muy útiles.
Inicialmente revisemos los derechos básicos de aprendizaje en MATEMÁTICAS para GRADO NOVENO:
DERECHOS BÁSICOS DE APRENDIZAJE GRADO NOVENO:
Utiliza los números reales (sus operaciones, relaciones y propiedades) para resolver problemas con expresiones polinómicas.
Evidencias de aprendizaje
- Considera el error que genera la aproximación de un número real a partir de números racionales.
- Identifica la diferencia entre exactitud y aproximación en las diferentes representaciones de los números reales.
- Construye representaciones geométricas y numéricas de los números reales (con decimales, raíces, razones, y otros símbolos) y realiza conversiones entre ellas.
Propone y desarrolla expresiones algebraicas en el conjunto de los números reales y utiliza las propiedades de la igualdad y de orden para determinar el conjunto solución de relaciones entre tales expresiones.
Evidencias de aprendizaje
- Identifica y utiliza múltiples representaciones de números reales para realizar transformaciones y comparaciones entre expresiones algebraicas.
- Establece conjeturas al resolver una situación problema, apoyado en propiedades y relaciones entre números reales.
- Determina y describe relaciones al comparar características de gráficas y expresiones algebraicas o funciones.
Utiliza los números reales, sus operaciones, relaciones y representaciones para analizar procesos infinitos y resolver problemas.
Evidencias de aprendizaje
- Encuentra las relaciones y propiedades que determinan la formación de secuencias numéricas.
- Determina y utiliza la expresión general de una sucesión para calcular cualquier valor de la misma y para compararla con otras sucesiones.
Identifica y utiliza relaciones entre el volumen y la capacidad de algunos cuerpos redondos (cilindro, cono y esfera) con referencia a las situaciones escolares y extraescolares.
Evidencias de aprendizaje
- Estima la capacidad de objetos con superficies redondas.
- Construye cuerpos redondos usando diferentes estrategias.
- Compara y representa las relaciones que encuentra de manera experimental entre el volumen y la capacidad de objetos con superficies redondas.
- Explica la pertinencia o no de la solución de un problema de cálculo de área o de volumen, de acuerdo con las condiciones de la situación.
Utiliza teoremas, propiedades y relaciones geométricas (teorema de Tales y el teorema de Pitágoras) para proponer y justificar estrategias de medición y cálculo de longitudes.
Evidencias de aprendizaje
- Describe y justifica procesos de medición de longitudes.
- Explica propiedades de figuras geométricas que se involucran en los procesos de medición.
- Justifica procedimientos de medición a partir del Teorema de Thales, Teorema de Pitágoras y relaciones intra e interfigurales.
- Valida la precisión de instrumentos para medir longitudes.
- Propone alternativas para estimar y medir con precisión diferentes magnitudes.
Conjetura acerca de las regularidades de las formas bidimensionales y tridimensionales y realiza inferencias a partir de los criterios de semejanza, congruencia y teoremas básicos.
Evidencias de aprendizaje
- Reconoce regularidades en formas bidimensionales y tridimensionales.
- Explica criterios de semejanza y congruencia a partir del teorema de Tales.
- Compara figuras geométricas y conjetura sobre posibles regularidades.
- Redacta y argumenta procesos llevados a cabo para resolver situaciones de semejanza y congruencia de figuras.
Interpreta el espacio de manera analítica a partir de relaciones geométricas que se establecen en las trayectorias y desplazamientos de los cuerpos en diferentes situaciones.
Evidencias de aprendizaje
- Describe verbalmente procesos de trayectorias y de desplazamiento.
- Explica y representa gráficamente la variación del movimiento de diferentes objetos.
Utiliza expresiones numéricas, algebraicas o gráficas para hacer descripciones de situaciones concretas y tomar decisiones con base en su interpretación.
Evidencias de aprendizaje
- Opera con formas simbólicas que representan cantidades.
- Reconoce que las letras pueden representar números y cantidades, y que se pueden operar con ellas y sobre ellas.
- Interpreta expresiones numéricas, algebraicas o gráficas y toma decisiones con base en su interpretación.
Utiliza procesos inductivos y lenguaje simbólico o algebraico para formular, proponer y resolver conjeturas en la solución de problemas numéricos, geométricos, métricos, en situaciones cotidianas y no cotidianas.
Evidencias de aprendizaje
- Efectúa exploraciones, organiza los resultados de las mismas y propone patrones de comportamiento.
- Propone conjeturas sobre configuraciones geométricas o numéricas y las expresa verbal o simbólicamente.
- Valida las conjeturas y explica sus conclusiones.
- Interpreta expresiones numéricas y toma decisiones con base en su interpretación.
Propone un diseño estadístico adecuado para resolver una pregunta que indaga por la comparación sobre las distribuciones de dos grupos de datos, para lo cual usa comprensivamente diagramas de caja, medidas de tendencia central, de variación y de localización.
Evidencias de aprendizaje
- Define el método para recolectar los datos (encuestas, observación o experimento simple) e identifica la población y el tamaño de la muestra del estudio. m Construye diagramas de caja y a partir de los resultados representados en ellos describe y compara la distribución de un conjunto de datos.
- Compara las distribuciones de los conjuntos de datos a partir de las medidas de tendencia central, las de variación y las de localización.
- Elabora conclusiones para responder el problema planteado
Encuentra el número de posibles resultados de experimentos aleatorios, con reemplazo y sin reemplazo, usando técnicas de conteo adecuadas, y argumenta la selección realizada en el contexto de la situación abordada. Encuentra la probabilidad de eventos aleatorios compuestos.
Evidencias de aprendizaje
- Diferencia experimentos aleatorios realizados con reemplazo, de experimentos aleatorios realizados sin reemplazo.
- Encuentra el número de posibles resultados de un experimento aleatorio, usando métodos adecuados (diagramas de árbol, combinaciones, permutaciones, regla de la multiplicación, etc.).
- Justifica la elección de un método particular de acuerdo al tipo de situación.
- Encuentra la probabilidad de eventos dados usando razón entre frecuencias.
Cartilla de enseñanza del ministerio de educación
En el siguiente enlace podrás encontrar y descargar la cartilla básica para nivel noveno de aprendizaje elaborada por el ministerio de Educación:
Igualmente si deseas trabajar con los derechos básicos de aprendizaje puedes enlazar con:
http://contenidosparaaprender.mineducacion.gov.co/G_9/M/index.html
PLAN DE TRABAJO
| Temáticas (semanas) | Contenidos |
| Elaborando ecuaciones algebraicas
(Trabajando la CANTIDAD, EL ESPACIO Y LA FORMA) |
Expresiones algebraicas en un texto
· Situaciones de suma y resta · Situaciones de multiplicación y división · Situaciones de potenciación y radicación |
| Expresiones algebraicas en geometría
· Agrupación de áreas · Áreas sombreadas · Triángulos · Teorema de Tales de Mileto · Teorema de Pitágoras Representaciones algebraicas · En la recta numérica · En el plano cartesiano · En perspectiva
|
|
| Simplificando ecuaciones algebraicas
(Trabajando EL CAMBIO Y LAS RELACIONES) |
Factorización |
| Solucionando ecuaciones algebraicas
(Trabajando EL CAMBIO Y LAS RELACIONES) |
Despeje de incógnitas |
| Métodos de solución ecuaciones de primer grado | |
| Métodos de solución ecuaciones simultáneas de primer grado | |
| Métodos de solución ecuaciones de segundo grado | |
| Estadística y probabilidad
(Trabajando la INCERTIDUMBRE) |
Expresiones algebraicas en Estadística
|
Trabajando la cantidad, el espacio y la forma
TEXTO Y CONTEXTO EN MATEMÁTICAS
Aprender a ver las matemáticas en toda situación real es una necesidad de quien intenta adquirir una experiencia motivadora en esta área. Reconocer que todo fenómeno de la naturaleza tiene una imagen abstracta, una representación matemática es al inicio algo difícil, pero no es imposible.
Desde que nos levantamos hasta que nos acostamos hacemos matemáticas. Tus movimientos durante el día son una ecuación donde el espacio, la velocidad, la trayectoria, el tiempo y un sinnúmero de variables afectan el desplazamiento de tu cuerpo, la materia que constituye tu cuerpo, tus átomos, moléculas se mueven constantemente a través de una danza electrónica que puede ser expresada mediante el lenguaje probabilista de las matemáticas.
Son muchas las situaciones en las que las matemáticas operan, para tu comprensión se han clasificado así : SITUACIONES PERSONALES que te afectan directamente, SITUACIONES EDUCATIVAS O LABORALES que se encuentran en el colegio o en un lugar de trabajo, SITUACIONES PÚBLICAS que se refieren a la comunidad y SITUACIONES CIENTÍFICAS que son las mas abstractas…por no decir difíciles (todo un reto para ti).
Para iniciarnos en este mundo de percepción matemáticas partiremos con el TEXTO ESCRITO como elemento para reconocer un proceso científico y aprender a mirar con los lentes de las matemáticas.
EJERCICIO DE LECTURA 1
1 PASO LEER CON ENTUSIASMO EL TEXTO: involucrarse con la lectura, encontrar elementos que llenen tu mente de intriga…
TOMADO DE: Cosmos en el atomismo de Leucipo y Demócrito: pluralidad, generación y corrupción. Guillermo Coronado. Editorial senderos, pág. 537.
En el anterior texto surgen interrogantes, palabras y personajes que desconocemos, debemos descartar lo que no es de interés directo del texto.
2. BUSCAMOS LAS IDEAS PRINCIPALES Y LOS CONCEPTOS PRINCIPALES

Cada párrafo tiene su idea principal, que entre otras características debe consolidar y sintetizar de manera coherente el contenido del párrafo.
Aparecen además conceptos de profundización como los que se encuentran en color naranja, algunos que simplemente los resuelves con un diccionario que te los re interpreta en color azul y otros que son meramente biográficos, históricos o geográficos para indagar.
3. INDAGAMOS Y PROFUNDIZAMOS EN LOS CONCEPTOS
LOS INFINITOS MUNDOS
El universo o Cosmos esta lleno de elementos, algunos representados por el hombre con ayuda de la ASTRONOMÍA y otros aún por descubrir. Desde ESTRELLAS, PLANETAS, SATÉLITES, NEBULOSAS, QUASARS, ESTRELLAS DE NEUTRONES, METEOROS, ASTEROIDES, COMETAS, etc. hasta las mas sofisticadas teorizaciones del espacio como AGUJEROS DE GUSANO, AGUJEROS NEGROS y otras.
Y matemáticamente que nos podría interesar? aquí te presento dos elementos ( pueden existir mas) que nos interesan matemáticamente:
LA FORMA DEL UNIVERSO

Tomado de: http://www.agenciasinc.es/Reportajes/La-foto-imposible-del-universo
Que nos muestra la GEOMETRÍA posible del Cosmos.
EL TAMAÑO DEL UNIVERSO
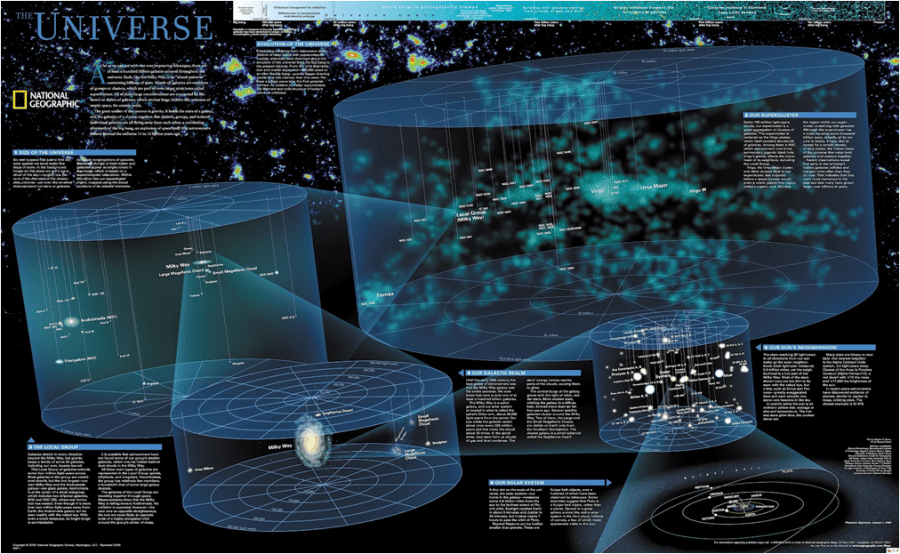
Tomado de: http://www.emiliosilveravazquez.com/blog/2013/10/23/la-masa-del-universo-la-inflacion-el-tamano%E2%80%A6ii/
Que no solo nos demuestra lo insignificante que somos en comparación del universo, sino que nos habla de MEDIDAS Y DISTANCIAS que son interés de las matemáticas.
EL ATOMISMO GRIEGO
Vale la pena pensar en esta épocas pasadas y en la capacidad que tenían algunas personas para abstraer en su mente conceptos que aún la ciencia maneja y profundiza cada día mas.
Hablamos de personajes como LEUCIPO, DEMÓCRITO, EPICURO Y LUCRECIO quienes concibieron el término ATOMO como respuesta a la pregunta fundamental: CUAL ES EL PRINCIPIO DE TODAS LAS COSAS?
A partir de ahí, han existido diferentes interpretaciones y representaciones GEOMÉTRICAS de el átomo:
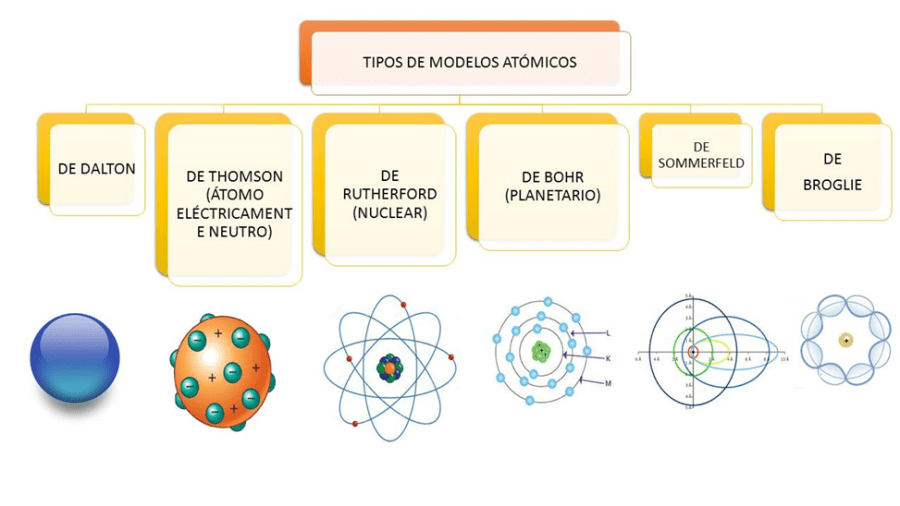
Tomado de: https://sites.google.com/site/proyectocabaga/modelos-atomicos
Esas formas y figuras geométricas que describen las órbitas de las partículas atómicas son de gran interés para las matemáticas.
Además podemos indagar en la GEOGRAFÍA de esta cultura:
![]()
http://jossoriohistoria.blogspot.com.co/2013/05/mapa-fisico-de-europa-mudo.html
Aquí no solo encontramos los conceptos matemáticos de ÁREA territorial, sino de PARALELOS Y MERIDIANOS que permiten la medición del TIEMPO y de las Zonas TÉRMICAS de la tierra. Todo lo que se puede expresar con la matemáticas y sus ecuaciones.
Y como un apunte adicional….mira cuantas partículas integran el átomo:
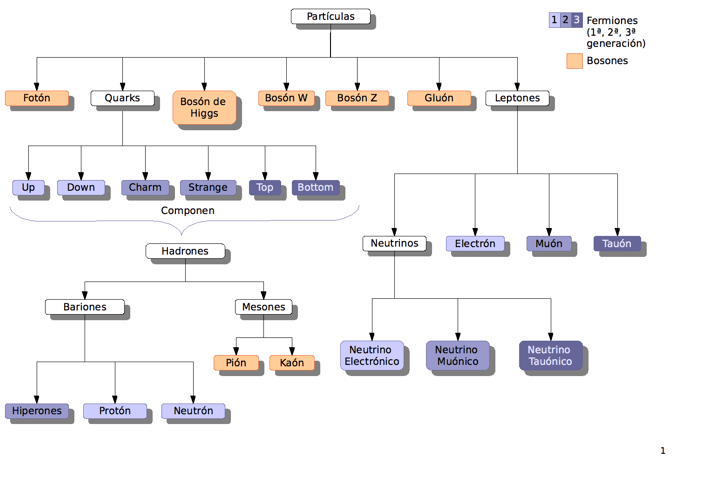
Tomado de: https://eltamiz.com/esas-maravillosas-particulas/
Muchas de ellas solo se pueden visualizar mediante las matemáticas.
Y continuando sobre los griegos otro tema a indagar que puede tener una connotación en las matemáticas es:
LA COSMOLOGÍA GRIEGA

y porque nos interesa tanto a los matemáticos este concepto?, pues entre otras cosas porque uno de estos personajes es PITAGORAS. Ahí te dejo la inquietud.
CONCEPTOS DE SIMPLE INTERPRETACIÓN
Con la ayuda del diccionario podemos entender algunas palabras que nos parecen de difícil comprensión
engendrar
Del lat. ingenerāre.
- tr. Dicho de una persona o de un animal: Dar vida a un nuevo ser. U. t. c. intr. Ya estáenedad de engendrar.
- tr. Causar, ocasionar, formar. U. t. c. prnl
perecedero, ra
- adj.Poco durable, que ha de perecer o acabarse.
- m. coloq. Necesidad, estrechez o miseria en las cosas precisas para el sustento humano
semejante
- adj.Que semeja o se parece a alguien o algo. U. t. c. s.
- adj.U. con sentido de comparación o ponderación. No es lícito valerse de semejantes medios.
- adj.U. con carácter de demostrativo, equivale a tal. No he visto semejante lío.
- adj.Geom. Dicho de una figura: Que es distinta a otra solo por el tamaño y cuyas partes guardan todas respectivamente la misma proporción.
- m. Semejanza, imitación.
- m. prójimo.
- m. desus. Símil retórico.
plural
Del lat. plurālis.
- adj.Múltiple, que se presenta en más de un aspecto. Alardeaba de su pluralconocimiento en el campo de las ciencias.
- adj.Gram. De número plural. Sintagma nominal plural.
- m. Forma gramatical que posee número plural.El plural de casa es casas.
4. m. Gram. número plural.
tesis
Del lat. thesis, y este del gr. θέσις thésis.
- f. Conclusión, proposición que se mantiene con razonamientos.
- f. Opinión de alguien sobre algo.
- f. Disertación escrita que presenta a la universidad el aspirante al título de doctor en unafacultad.
- f. Mús. Golpe en el movimiento de la mano con que se marca alternativamente elcompás.
unicidad
- f. Cualidad de único
Tomado de: http://dle.rae.es
CONCEPTOS BIOGRÁFICOS
Esos conceptos te corresponden indagarlos, descubre quienes fueron estos personajes y porque están unidos en este texto.
4. ELABORAMOS UN MAPA CONCEPTUAL DEL TEXTO
En el proceso de lectura consciente no hay nada mejor para guardar nuestras ideas que un mapa conceptual que recoja en forma condensada la lectura:

SITUACIONES REALES Y EXPRESIONES MATEMÁTICAS
Cada vez que se enuncia un problema o DESCRIBIMOS UNA SITUACIÓN DEL MUNDO QUE NOS RODEA escribimos un texto, un texto que se puede interpretar en ecuaciones, si reconocemos las variables y los valores.
Iniciemos con algo sencillo:
Si yo digo EN LA MALETA TENGO CINCO COLORES Y UN LAPIZ
Podría interpretar la MALETA como el lugar donde se encuentran unidos los COLORES y el LAPIZ.
Los COLORES puedo interpretarlos como una variable, la letra que yo escoja, puede ser la C que es la primera de la palabra COLORES, es decir que en la MALETA tengo 5C (5 colores).
El LAPIZ igualmente lo puedo interpretar y representar con la L, es decir que en la MALETA tengo 1L (1 Lápiz).
Igualmente podría deducir que en la MALETA tengo en total la UNION de los 5 Colores y 1 Lápiz, es decir una SUMA.
De Esta forma el TEXTO:
EN LA MALETA TENGO CINCO COLORES Y UN LAPIZ = 5C + 1L = 5C + L
Recordando que el número 1 antes de una letra según las características del álgebra no se escribe.
A partir de este hecho, TODA SITUACIÓN PUEDE LLEVARSE A UNA EXPRESIÓN MATEMÁTICA.
Vamos entonces a escribir varios texto en forma de expresión matemática, aquí toca que recuerdes cada operación matemática que has realizado hasta el momento.
SITUACIONES QUE IMPLICAN SUMAS Y RESTAS
1) La suma de las edades de A y B es 56 años, B tiene 4 años menos que A.
A+B= 56 A – 4 = B
2) Pagué 300 por un par de medias, una corbata y un libro. La corbata costó 40 más que el par de medias y 120 menos que el libro.
M = par de medias (Aquí estamos identificando las variables con una letra!)
C = Corbata
L = Libro
M + C + L = 300
C = M + 40
C = L – 120
3) La suma de tres números enteros consecutivos es de 200.
A = número menor
B = número intermedio (B = A + 1)
C = número mayor (C = B + 1) (C = A + 2)
A + B + C = 200
SITUACIONES QUE IMPLICAN MULTIPLICACIÓN Y DIVISIÓN
4) La edad de A es el doble que la de B y ambas edades suman 20 años.
A = 2B A + B = 20
5) Se compran huevos, queso y leche por $3500. La leche costó el doble que el queso y el queso costó el triple que los huevos.
X= precio de los huevos
Y= precio del queso
Z= precio de la leche
X + Y + Z = 3500
Z = 2Y
Y = 3X
EJERCICIOS PARA TRABAJAR 1:
6) La edad de José es la mitad de la de Pedro, y la de Juan el triple que la de José. Y las tres edades suman 125 años.
7) Dividir 150 en dos partes tales que el triple de la parte menor equivale al duplo de la mayor.
8) La edad de A es el doble de la B y hace 15 años la edad de A era el triple de la de B.
9) Se compraron 60 frutas entre naranjas y manzanas. Cada naranja costó $40 y cada manzana $85. El total de la compra fue de $5600.
10) El duplo de un número excede en 30 al tercio del mismo número
11) La suma de dos números es 50 y si el mayor se divide por el menor, el cociente es 2 y el residuo 5.
12) Juan tenía cierta suma de dinero. Gastó $20 en libros y los dos tercios de lo que le quedaba en lápices. Le quedan todavía $35.
13) La edad de X es la mitad de la de Y, y hace 10 años la edad de X era cinco cuartos de la edad de Y.
14) La longitud de un rectángulo excede al ancho en 3 metros. Si cada dimensión se aumenta en 2 metros, el área aumentaría en 60 metros cuadrados.
15) La cifra de las decenas de un número de dos cifras excede en 2 a la cifra de las unidades y si el número se divide por la suma de sus cifras, su cociente es 5.
Luego de realizar los anteriores ejercicios, puedes consultar sus soluciones aquí: soluciones ejercicios 1
SITUACIONES QUE IMPLICAN POTENCIACIÓN Y RADICACIÓN
16) X es dos años mayor que Y y la suma de los cuadrados de ambas edades es 100 años
X = Y + 2

17) El producto de dos números es 30 y su cociente es 5.
X = primer número
Y = segundo número
XY = 30
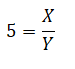
LECTURA RECOMENDADA:
Vamos a leer EL HOMBRE QUE CALCULABA de MALBA TAHAN. Son Dos capítulos por semana que debes leer y presentarlos SUBRAYADOS, TU LISTADO DE CONCEPTOS INDAGADOS Y TU MAPA CONCEPTUAL, ahí te dejo el enlace para que lo descargues y leas:
Otro texto que trabajaremos durante el semestre y que es de mucha utilidad para ti es el ÁLGEBRA DE BALDOR, aquí te dejo el enlace para que la tengas en tu casa:
LECTURA 2 DE RECUPERACIÓN
Si no realizaste el trabajo de lectura anterior y deseas recuperar este logro, debes leer adicionalmente al texto anterior y realizar iguales trabajos:
Recuerda que siempre tienes la oportunidad de ser mejor, pero cuesta un esfuerzo.
LECTURA 3 DE RECUPERACIÓN 3
Para quienes aún deben todas las lecturas, primero deben hacerlas( Hombre que calculaba capítulos 1,2,3 y 4) ….y luego el trabajo de recuperación 1 y luego el trabajo de recuperación dos que es el siguiente:
LECTURA 4 DE RECUPERACIÓN
Además de las anteriores se adiciona a la lista de recuperación esta lectura que pueden descargar en el siguiente enlace:
el-senor-del-cero-maria-isabel-molina1
SIMPLIFICANDO LAS EXPRESIONES MATEMÁTICAS.
Es cierto que mediante la suma, resta y otras operaciones simples podemos reducir las expresiones matemáticas teniendo en cuenta los principios del álgebra en cuanto a la semejanza de términos.
Sin embargo la FACTORIZACIÓN es uno de los métodos más empleados en este trabajo de simplificación.
Recordemos los casos de FACTORIZACIÓN
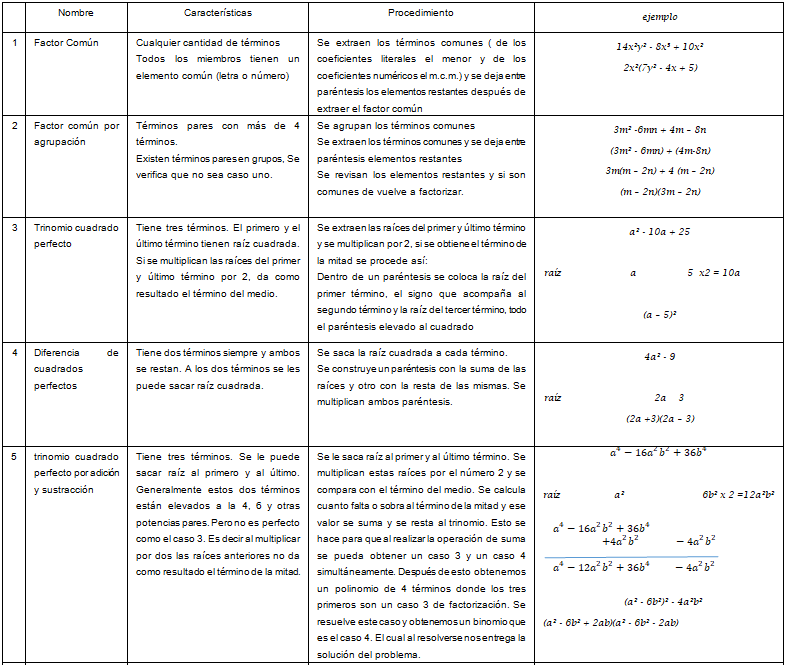
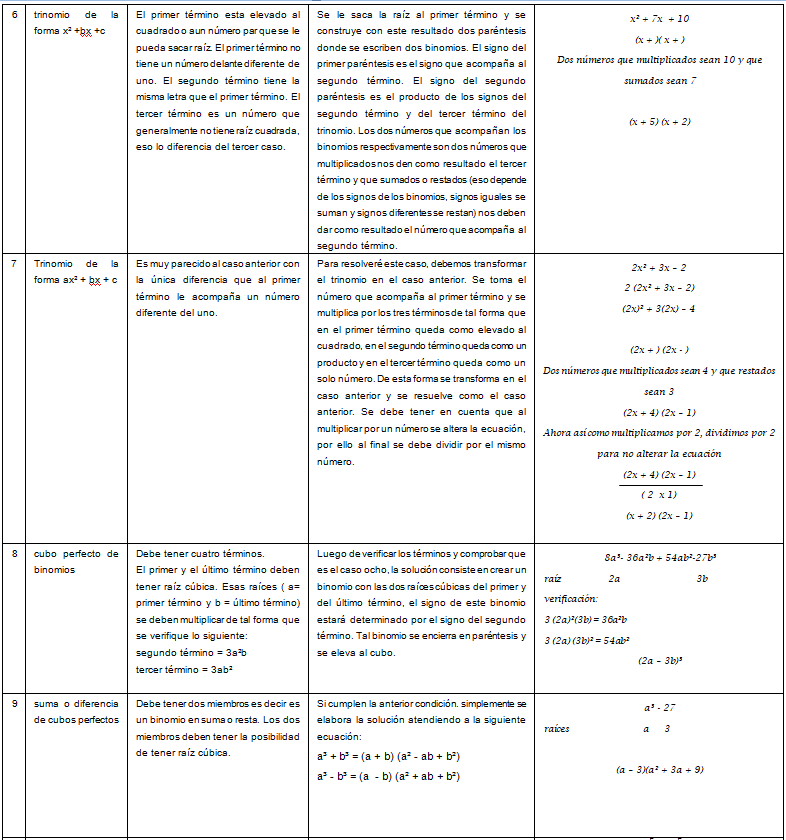

Solucionando problemas a través de las ecuaciones algebraicas
RESOLVIENDO LAS EXPRESIONES MATEMÁTICAS
Una de las actividades más reconocidas de las matemáticas es el hallazgo de soluciones a los problemas que se derivan de las expresiones matemáticas que representan el MUNDO REAL y sus SITUACIONES.
DESPEJANDO INCÓGNITAS
Una de las formas de encontrar el valor de las variables desconocidas (incógnitas) es mediante el procedimiento de DESPEJE, el cual consiste en separar una variable de otras a través de operaciones contrarias a las que existen entre ellas.
CASOS DE OPERACIONES DE SUMA Y RESTA
EJEMPLO :Despejar x de la ecuación:
x + 4 = 2x
la x de los términos de la izquierda se traslada a la derecha y cambia de signo ( el que suma pasa a restar).
4 = 2x – x
se simplifican los términos de la derecha por ser semejantes.
4 = x
CASOS DE OPERACIONES DE MULTIPLICACIÓN Y DIVISIÓN
EJEMPLO :Despejar de la ecuación la letra y:

el número 5 del denominador de los términos a la izquierda pasa a multiplicar al 9 que es el término de la derecha. (el que divide pasa a multiplicar)
3y = 45
el número 3 que acompaña la letra y la multiplica pasa dividir al número 45 que es el término de la derecha. (el que multiplica pasa a dividir)

CASOS DE OPERACIONES CON POTENCIACIÓN Y RADICACIÓN
EJEMPLO: Despejar de la ecuación la letra a:

La letra b que multiplica a la letra a, pasa a dividir al número 27.
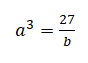
La potencia cúbica pasa como una raíz cúbica al miembro de la derecha
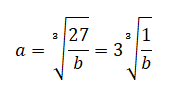
EL TEXTO GRÁFICO: LA GEOMETRÍA Y LAS EXPRESIONES MATEMÁTICAS
Todo objeto del mundo tiene una configuración llamada FORMA que es considerada en la ciencia como una propiedad o una variable de algo que llamamos MATERIA en cualquiera de sus estados FÍSICOQUIMICOS.
La comprensión que hace de la naturaleza la ciencia, acerca de este concepto de FORMA (Ver CONCEPTUALIZANDO1) es tratado por la matemática a partir de la GEOMETRÍA. Para nuestro interés realizaremos mediciones en una dimensión (perímetros), en dos dimensiones (áreas) y en tres dimensiones (volumen) de la FORMA de ciertos objetos.
EL ORIGEN DE LA FORMA
Así como cualquier TEXTO parte de un CONTEXTO real que está inmerso en las palabras y que podemos escribir en el TEXTO ABSTRACTO DE LAS MATEMÁTICAS. La FORMA y la MEDIDA tiene su CONTEXTO en la NATURALEZA.

Tomado de: https://www.elconfidencial.com/multimedia/album/tecnologia/2015-02-28/las-matematicas-de-la-naturaleza_719480/
¿Qué hace que la naturaleza construya en una determinada forma?
Para responder a esa pregunta acudo a las palabras de mi maestra Janine Benyus cuando nos habla de la BIOMÍMESIS:
Existe una estabilidad dinámica entre todos los seres naturales, cuyas funciones, estructura y vida presentan un equilibrio, esto es debido a que:
• Funcionan con la luz solar.
• Utilizan únicamente la energía necesaria.
• Adecúan forma y función.
• Reciclan todo.
• Recompensan la cooperación.
• Acumulan diversidad.
• Contrarrestan los excesos desde el interior.
• Utilizan la fuerza de los límites.
• Aprenden de su contexto.
• Cuidan de las generaciones futuras.
Bajo las anteriores reglas la naturaleza construye las FORMAS y las DIMENSIONES del mundo.
Tratemos entonces de reconocer estas cualidades en su diseño.
LAS FORMAS ESPIRALES: SERIES DE FIBONACCI, SECCIONES ÁUREAS

Tomado de: http://www.matematicasdigitales.com/matematicas-en-la-naturaleza/

Tomado de: https://oldearth.wordpress.com/2008/09/11/%C2%BFson-los-huracanes-consecuencia-de-un-diseno-inteligente/
LAS FORMAS ESPIRALES: ESPIRALES LOGARÍTMICAS

Tomado de: http://www.matematicasdigitales.com/matematicas-en-la-naturaleza/
LAS FORMAS GEOMÉTRICAS: POLÍGONOS REGULARES

Tomado de: http://ciencia-bizarra.blogspot.com.co/2014/06/matematicas-y-naturaleza-i.html

Tomado de: http://matemolivares.blogia.com/temas/matematicas-y-geometria-en-la-naturaleza..php
LOS SINTAGMAS EN LA NATURALEZA



Tomado de: https://carlosnacazona.wordpress.com/2010/06/22/sintagmas-de-la-naturaleza/
Los POLÍGONOS IRREGULARES

Tomado de: http://matemolivares.blogia.com/temas/matematicas-y-geometria-en-la-naturaleza..php
LOS REFLEJOS DE LA NATURALEZA: LAS SIMETRÍAS
Tomado de: http://www.tipos.co/tipos-de-simetria/

Tomado de: https://www.stillnessspeaks.com/zen-practice-henry-shukman/
EL CRECIMIENTO NATURAL: LOS FRACTALES

Tomado de: http://pijamasurf.com/2010/09/top-11-patrones-fractales-en-la-naturaleza/

Tomado de: http://angelfebrero.blogspot.com.co/2005/12/formas-fractales-en-la-naturaleza.html

http://digitalhiggs.com/index.php/expresion-digital/item/437-la-perfeccion-infinita-de-la-naturaleza-fractales

Tomado de: https://www.flickr.com/photos/roddh/307187374

Tomado de: https://articulosletraviva.wordpress.com/2010/04/19/matematicas-en-la-naturaleza/

Tomado de: https://lamaletademaxweb.wordpress.com/2017/07/17/fractales/

Tomado de: https://steemit.com/science/@konstantin/sacred-geometry-in-nature-fractals-fibonacci-golden-section-or-proportion-of-god
Todas las FORMAS Y DIMENSIONES NATURALES tienen una razón de ser, no hay capricho en la naturaleza. La MATEMÁTICA es testigo de la perfección de la naturaleza.
Es a partir de las FORMAS y DIMENSIONES NATURALES que el hombre crea sus primeras figuras geométricas y sus primeras unidades de medición.

Tomado de: http://naturalezadealbolote.blogspot.com.co/2013/04/matematicas-en-la-naturaleza.html
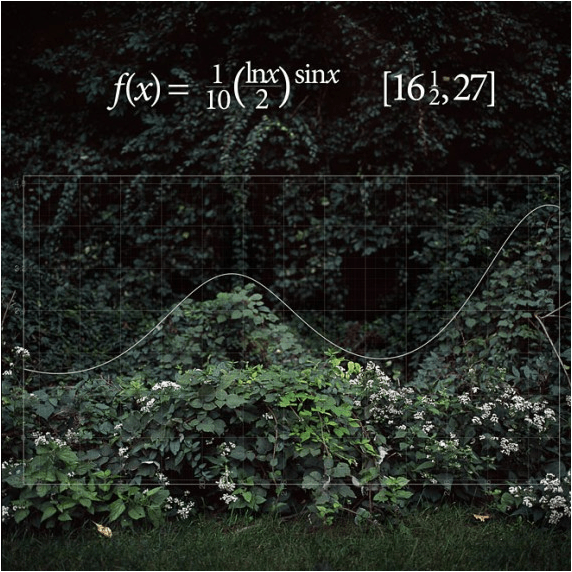
Tomado de: https://www.fayerwayer.com/2010/02/fotografia-todo-en-la-naturaleza-son-matematicas/
Se hace necesario que hagamos un recorrido por estas diversas formas de ABSTRAER la FORMA y LA DIMENSIÓN NATURAL. Empecemos por el mundo de la PRIMERA Y SEGUNDA DIMENSIÓN:
PERÍMETROS y ÁREAS
Inicialmente recordemos que un PERÍMETRO es la suma LINEAL de todos los lados que forman una figura geométrica, el concepto básico se calcula mediante las fórmulas que se encuentran en la siguiente figura, pero tú igualmente lo puedes deducir.
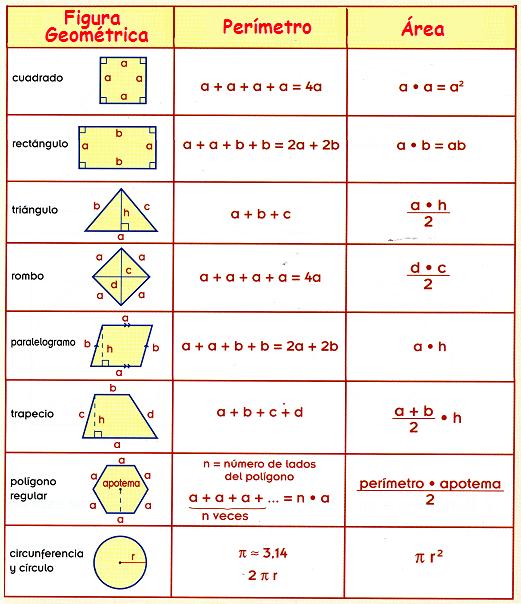
Tomado de: https://www.slideshare.net/AmarinoMoisesLaraGonzalez/formula-poligonos
En los POLÍGONOS REGULARES es decir aquellos cuyos lados son iguales, simplemente el PERÍMETRO puede ser hallado sumando el tamaño de cada lado (que es igual) un número de veces igual a su número de lados. Esta operación de SUMA se puede SIMPLIFICAR en una operación de MULTIPLICACIÓN para este caso.
En los TRIÁNGULOS hay varias formas de obtener el PERÍMETRO:
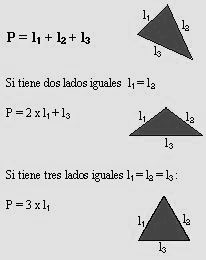
Tomado de: https://matematica.laguia2000.com/general/perimetro-de-figuras-plana
Que tanto sabemos del TRIANGULO??
TALES DE MILETOS y la fuente de inspiración
Algunas veces pensamos que la ciencia nace de los genios, de personas predestinadas y aún de países cuya tradición científica se remonta siglos atrás, sin embargo no todo es producto de un destino demarcado; como veremos en está historia… a veces los genios no nacen “como se cree popularmente” sino que se hacen.
La historia biográfica de TALES DE MILETOS es de fácil acceso en cualquier página de internet, lo que interesa a la física tiene que ver con el proceso de generación de ciencia, proceso que inicia este personaje en su juventud de acuerdo a variadas referencias (Diaz, 2002, p. 13) como comerciante en su juventud y que le permite viajar por países de frontera a su ciudad natal Miletos ubicada en pleno centro del imperio Griego : la península de anatolia (actual Turquía), ya podemos imaginarnos este universo rodeado de transeúntes que venían de oriente hacia occidente y viceversa, trayendo historias, inventos y porque no ciencia.
La visión de Hecateo en su mapa de un mundo circular y armónico, influiría cualquier concepción juvenil y animaría a un viajero a desear rodear ese mundo.
TALES DE MILETOS viaja a Caldea y a Egipto donde recibirá la influencia de estas cosmologías en su pensamiento tal como afirma Josefo ((D-K 11 A 11) Josefo, Contra Apionem I, 2):
“Todos están de acuerdo en que los primeros que entre los griegos filosofaron sobre las cosas celestes y divinas, como Ferécides de Siro, Pitágoras y Tales, fueron discípulos de los egipcios y caldeos”(Tomado de: http://www.filosofia.org/cur/pre/talesfyt.htm)
En Caldea, reino de Mesopotamia no era extraño que el estudio por la astronomía llegara a Tales, los caldeos eran prácticamente en este aspecto adoradores de los planetas como se afirma en algunos pasajes de la Biblia (Martin, 2009, p. 251), la impresionante distribución del espacio geométrico aplicado a la construcción de estas ciudades en Mesopotamia nos hace dar cuenta de la ordenada aparición de la civilización.
Una escritura como la cuneiforme y las tablillas que nos muestran tantos indicios de civilización solo confirman la influencia del pensamiento oriental en el pensamiento occidental.

Observar en estos documentos, de los cuales posiblemente Tales de Miletos también tuvo conocimiento, nos puede abrir la mente al origen de muchas posturas de los griegos de origen Fenicio.

Tablilla de Sitchin. Tomado de : http://www.taringa.net
Observar la tablilla anterior nos hace nuevamente pensar en el sistema heliocéntrico que tanto defendería Giordano Bruno, Copérnico y Galileo Galilei entre otros. Las culturas Mesopotámicas a ciencia cierta tenían un conocimiento del cosmos que influiría a todo occidente.
Como si fuera poco, Tales de Miletos viaja a Egipto. Las impresionantes pirámides serán la inspiración de su primer teorema.
La siguiente infografía nos brinda una relación entre el teorema de tales de miletos y su analogía con las pirámides:

El triángulo es desde tiempos muy remotos una figura esencial en el estudio de la matemáticas, la geometría y aunque no lo creas en la filosofía y hasta las religiones.
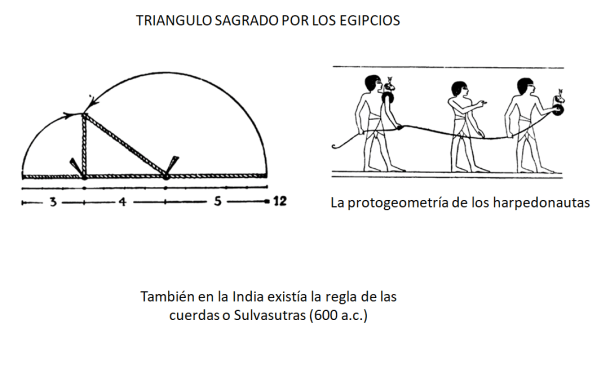
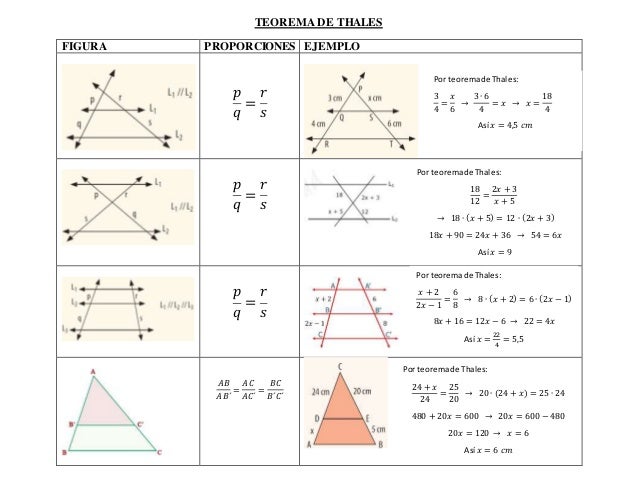
Tomado de: https://www.slideshare.net/luisubiabre1/tabla-teorema-de-thales
EJERCICIOS 1
Ejercicios: https://www.slideshare.net/xto316/teorema-de-thales-prueba-rocket?next_slideshow=1
PITAGORAS y su teorema
aunque PITAGORAS DE SAMOS (569 – 475 a.c.) haría muy famosa esta figura geométrica ya existían vestigios de su fama en otras culturas:


Pitagoras es conocido por todos y su ecuación ( esta ecuación es fundamental en la física y la trigonometría):
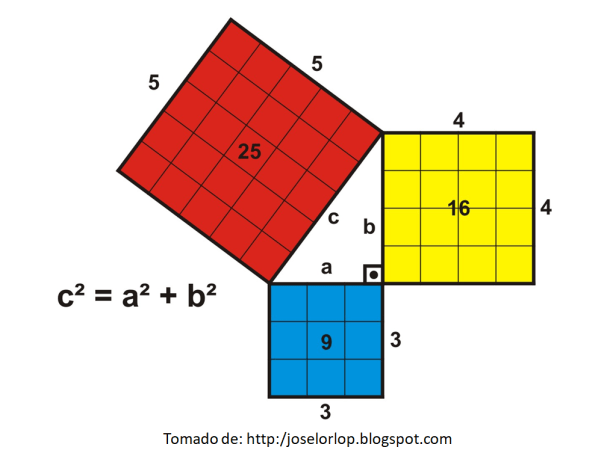
Y estudiada durante mucho tiempo:

Luego de la historia, calculemos el valor de los lados del triángulo rectángulo, empleando el teorema de Pitágoras.
EJERCICIOS 2

Tomado de: http://demostremosloaprendido.blogspot.com.co/2014/08/teorema-de-pitagoras.html
CURIOSIDADES DE LA GEOMETRÍA PLANA

Tomado de: https://www.pinterest.cl/pin/296956169171548402/
HIPASO DE METAPONTO….y el teorema de pitágoras
Usualmente se suele pensar que el nombre de los teoremas es debido a su autor. Si escuchamos continuamente que se llama teorema de PITÁGORAS es porque este personaje lo inventó.
Sin embargo como vimos en las imágenes anteriores mucho tiempo antes del nacimiento de PITÁGORAS esta relación entre los lados de un triangulo rectángulo y su hipotenusa era ya estudiada. Mas curioso aún que en la famosa ESCUELA PITAGÓRICA pudiese ser posible que el verdadero autor del teorema no fuera PITÁGORAS sino uno de sus discípulos, un tal HIPASO DE METAPONTO. La verdad queda para que tu la indagues.
En este capítulo me interesa que sepas que HIPASO DE METAPONTO se hizo una pregunta bastante interesante con el teorema…¿ Si los lados del triangulo rectángulo tienen el mismo valor a la unidad, cuanto vale la hipotenusa?

Tomado de: http://matesparasaltamontes.blogspot.com.co/2016/02/hipaso-de-metaponto.html
Pues como se puede ver en la imagen al aplicar el famoso teorema nos encontramos conque el resultado es una raíz, del número dos en este caso.

Cuyo resultado es un número irracional, es decir un número primero que no tiene fin, y segundo que no tiene una secuencia repetitiva, es decir que no sabemos por lógica que numero sigue en su secuencia de resultados.
¿pero entonces se preguntó HIPASO DE METAPONTO como es posible que dos números enteros ( 1 en cada lado del triangulo), dos números considerados perfectos… nos de como resultado un número irreconocible, un número que no se puede medir?
Y mas aún nos preguntamos y ¿como es posible que lo podamos dibujar en una recta numérica sino tiene fin, es decir es inconmensurable? pues bien si se puede…aqui se ve su representación gráfica:

Tomado de: http://emaspi2eso.blogspot.com.co/2010/05/
Construimos sobre el plano cartesiano un triangulo con lados de valor unitario y su diagonal (hipotenusa) proyectada con ayuda de un compás se transforma en el valor raiz de dos solicitado. Lo mismo podemos hacer con otros números irracionales:

Y de esta manera lo hacemos sucesivamente con diferentes números irracionales:
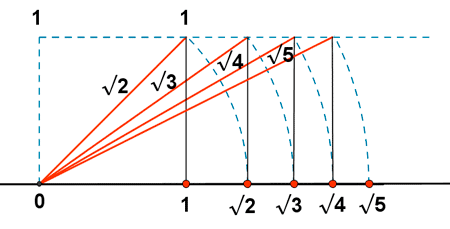
Tomado de: http://todomaths4eso.blogspot.com.co/p/blog-page.html
e incluso podemos crear una espiral con estos valores:

Tomado de: http://todomaths4eso.blogspot.com.co/p/blog-page.html
INDAGACIÓN 1
Tenemos dos números irracionales que esperamos indagues a cabalidad, desde quien lo descubre…hasta su forma de representación en la recta numérica:


ÁREA SOMBREADA
Con el dato de la tabla de áreas para figuras geométricas podemos calcular el área de diversas figuras:
EJEMPLO
Calcular el área sombreada de la figura. Como observamos el área gris o sombreada se obtiene al restar el área de un cuadrado de 8 cm de lado y el área de dos mitades de un círculo cuyo radio es de 4 cm:

EJERCICIOS 3

Tomado de: https://www.slideshare.net/asteteli/areas-sombreadas-57320341

Tomado de: https://www.pinterest.es/pin/185351340891950872/
INTERPRETACIÓN GEOMÉTRICA DE EXPRESIONES ALGEBRAICAS
Cuando sustituimos los valores numéricos de los lados de una figura geométrica por expresiones algebraicas obtenemos una nueva interpretación de la geometría:
EJEMPLO 1 CALCULAR EL PERÍMETRO:
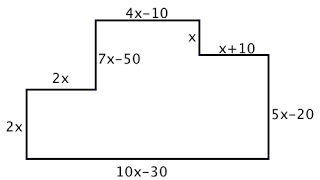
Tomado de: http://mate2tec31.blogspot.com.co/2012/11/cual-es-el-perimetro-de-la-siguiente.html
Elaboramos un polinomio para sumar los lados de la figura:
(2x) + (2x) + (7x-50) + (4x-10) + (x) + (x+10) + (5x-20) + (10x-30)
Resolvemos los paréntesis y agrupamos los términos:
2x +2x +7x +4x +x +x +5x +10x -50 -10 +10 -20 -30
Realizamos las operaciones indicadas y obtenemos el resultado que es un binómio:
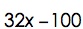
EJEMPLO 2 CALCULAR EL ÁREA

En la figura anterior vemos que al agrupar cada área independiente obtenemos una sola figura geométrica cuya expresión algebraica es un trinomio, caso 7 de factorización.
EJEMPLO 3 CALCULAR EL ÁREA SOMBREADA

Como se puede observar el área sombreada es el resultado de la resta entre el área del rectángulo y los 4 cuadrados de las esquinas. Luego se factoriza caso 1 y se aplica caso 4 para obtener el resultado presentado.
LA TERCERA DIMENSIÓN : VOLUMEN
Repasamos este tema de octavo nuevamente. Las tres dimensiones, es la expresión que involucra el conocimiento de los objetos con volumen, para los cuales existen ya fórmulas para su cálculo:

Tomado de: https://mauriciomedinasierra.wordpress.com/primer-corte/conceptos/volumen/tabla-de-areas-y-volumenes-figuras-geometricas/
También se puede consultar: http://blogdecarina.blogspot.com.co/2014/02/volumen-cuerpos-geometricos.html
En la tabla anterior se observa además del nombre y la forma de la figura tridimensional, el desarrollo del sólido correspondiente para su elaboración a partir de una superficie plana. Existe una columna donde aparece el cálculo del área superficial de cada figura y la ecuación del cálculo del volumen.
Gracias a estos valores podemos hacer cálculos con expresiones matemáticas:
EJEMPLO 1
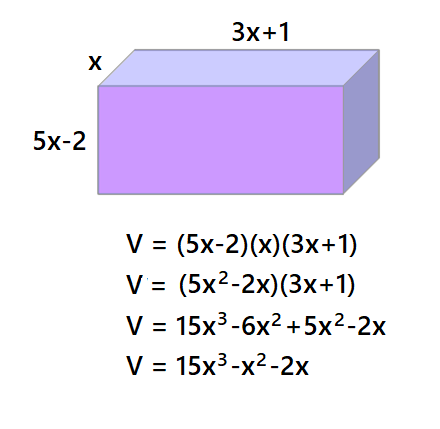
Tomado de: http://cremc.ponce.inter.edu/algebrageometrica/taller1.htm
EJEMPLO 2
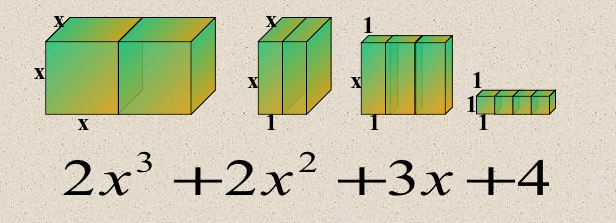
Tomado de: https://es.slideshare.net/MATEMATICASEEMM/polinomios-2700548
EJERCICIO 4
Calcular el volumen y simplificar la expresión algebraica.

Tomado de: http://ww2.educarchile.cl/PORTAL.HERRAMIENTAS/SIMCE2006/Ejercicios/Diagnostica_Segundo.aspx?sector=2&nivel=2&id_Eje=98
REPRESENTACIÓN VOLUMETRICA MEDIANTE PERSPECTIVA
Existen muchas formas de representar mediante el empleo del DIBUJO TÉCNICO una figura de volumen. Hagamos un alto y observemos este desarrollo de la geometría en el ARTE. Consideraremos solo tres formas de representación:
PERSPECTIVA CABALLERA
Esta forma de representación maneja una de las caras del objeto a 45 grados.

Tomado de: https://es.wikipedia.org/wiki/Perspectiva_caballera
PERSPECTIVA ISOMÉTRICA
Esta se caracteriza por representar un objeto en posición angular de 120 grados entre sus ejes

Tomado de: https://es.wikipedia.org/wiki/Proyecci%C3%B3n_isom%C3%A9trica
TALLER DE MODELOS ISOMÉTRICOS
Realizar el siguiente taller: Obteniendo las tres vistas principales de cada uno de los modelos isométricos. No es necesario elaborar las figuras. Puedes hacer hasta cuatro soluciones por hoja de papel milimetrado. Dale click al enlace siguiente, descarga e imprime el taller. Lo resuelves en hojas de papel milimetrado:
taller modelos isométricos recuperación
PERSPECTIVA DE PUNTOS DE FUGA
Esta se presenta en tres tipos:
PERSPECTIVA DE UN PUNTO DE FUGA:
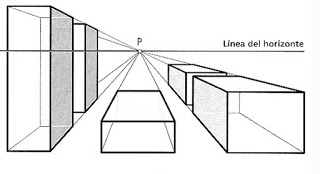
Tomado de: http://plasticandoenlaeso.blogspot.com.co/2015/06/perspectiva-conica-con-1-punto-de-fuga.html
PERSPECTIVA DE DOS PUNTOS DE FUGA

Tomado de: http://mumng.blogspot.com.co/2014/08/97-fundamentos-de-diseno-dibujo-de.html
PERSPECTIVA DE TRES PUNTOS DE FUGA

Tomado de: http://infocristobalina9.blogspot.com.co/2016/05/ejercicio-3-perspectiva-dos-puntos-de.html
HACIENDO UN PARÉNTESIS
Bien hasta este momento tu mente ha realizado un proceso que en matemáticas recibe el nombre de MATEMATIZACIÓN, si sé que es un poco complicado y por eso no empece a explicarte las matemáticas bajo este concepto. Pero es justo y necesario que te enteres como trabaja en tu cerebro todas las cosas que te cuento.
La MATEMATIZACIÓN implica en primer lugar traducir los problemas desde el mundo REAL al mundo MATEMÁTICO, este proceso se llama MATEMATIZACIÓN HORIZONTAL (según los científicos) y consta de varias actividades en tu mente:
- Identificar que tanto de matemáticas tiene un problema del mundo real
- Representar el problema de manera diferente
- Comprender la relación entre la situación real y la representación simbólica de la misma
- Encontrar regularidades, relaciones y patrones
- Reconocer semejanzas con otros problemas ya conocidos
- Traducir el problema a un modelo matemático
- utilizar las herramientas y recursos adecuados para su solución
En segundo lugar ( LUEGO DE LEER EL CAPÍTULO: EN BUSCA DE LAS SOLUCIONES, que se encuentra a continuación) que espero que realices un proceso de MATEMATIZACIÓN VERTICAL, es decir una vez tengas esa expresión matemática que representa el problema apliques las destrezas operacionales de la matemáticas para ir mas allá:
- Utilizar diferentes representaciones
- Usar el lenguaje matemático y sus operaciones
- Ajustar los modelos matemáticos
- Argumentar
- Generalizar
- Entender los límites de los conceptos matemáticos
- Reflexionar sobre los argumentos matemáticos, explicar y justificar los resultados
- Comunicar el proceso y la solución
- Criticar el modelo y sus límites, para mejorarlo.
EN BUSCA DE LAS SOLUCIONES
SOLUCIONANDO PROBLEMAS DE UNA INCÓGNITA MEDIANTE DESPEJE
De las situaciones vistas anteriormente las planteadas los ejercicios 10 y 12 tienen una sola variable que a su vez es la incógnita, mediante despeje podemos hallar su valor:
EJEMPLO 1 : Resolver el Ejercicio 10 presentado anteriormente
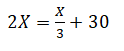
Pasamos los miembros con letra a la izquierda (Cambiando su signo)

Realizamos las operaciones
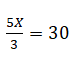
Despejamos la letra x, el 3 pasa a multiplicar y el 5 a dividir
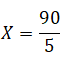
EJEMPLO 2: Resolver el Ejercicio 12 presentado anteriormente

SOLUCIONANDO PROBLEMAS DE DOS INCÓGNITAS
Cuando tenemos mas de una incógnita por resolver ( ejercicio 1 por ejemplo) la situación es diferente por cuanto debemos tener como mínimo un número de ecuaciones igual al número de incógnitas, lo cual nos garantiza tener UNA SOLUCIÓN ÚNICA para cada incógnita. En caso que el número de ecuaciones sea menor que el número de incógnitas podemos tener VARIADAS SOLUCIONES para la misma incógnita.
Un problema de este caso sería:
El perímetro de un cuarto rectangular es de 18 m, y 4 veces el largo equivale a 5 veces el ancho. Hallar las dimensiones del cuarto y su área.
Debemos recordar primero que es un perímetro y un área para el caso del rectángulo:

Tomado de: http://slideplayer.es/slide/1023628/
Las variables serían:
b= largo
a= ancho
Las expresiones algebraicas que representan mediante ecuaciones el problema serían:
(1) 2a + 2b = 18
(2) 4b = 5a
Bien, existen 5 formas de solucionar este tipo de problemas:
IGUALACIÓN

SUSTITUCIÓN

REDUCCIÓN

DETERMINANTES

GRÁFICO


En el lugar donde se cruzan las dos líneas ( cada línea representa una expresión algebraica) es la solución al problema.
SOLUCIONANDO EXPRESIONES ALGEBRAICAS DE SEGUNDO Y OTROS GRADOS
Cuando las expresiones algebraicas no son de primer grado se aplican otras soluciones.
ECUACIONES DE SEGUNDO GRADO
Aunque hay mas tipos de soluciones para estas ecuaciones, aquí te explicaré dos tipos:
MEDIANTE LA ECUACIÓN DEL TÉRMINO DISCRIMINANTE
El término DISCRIMINANTE aunque parezca malo, nos permite en la matemática «desechar» o no un problema de segundo grado. Si el resultado de este término es negativo lamentablemente no hay solución REAL a nuestro problema (ingresamos al mundo de los NÚMEROS COMPLEJOS), si el resultado nos da cero entonces hay solo una solución, pero si el resultado es positivo significa que tenemos dos respuestas.
Bien recordemos una expresión algebraica de segundo grado (la mas general un caso 7 de factorización):
ax 2 + bx + c = 0
al cual le podemos calcular el término discriminante mediante la ecuación:
b 2 – 4 ac
La fórmula cuadrática nos permite entonces hallar las soluciones posibles:

Obviamente los resultados obtenidos tienen una REPRESENTACIÓN GRÁFICA que en este caso se llama PARÁBOLA.
cuando el DISCRIMINANTE ES POSITIVO (tenemos dos soluciones o intercepciones en el eje (x)), como ejemplo ( las gráficas son tomadas de :https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/discriminant)

cuando el DISCRIMINANTE ES CERO (tenemos una solución o intercepción con el eje (x) ), como ejemplo:

y cuando el DISCRIMINANTE ES NEGATIVO no hay punto de corte con el eje (x), como ejemplo:

entonces resolvamos un caso de estos:
EJEMPLO
Resuelva la ecuación cuadrática.
x 2 – x – 12 = 0
Aquí a = 1, b = – 1, y c = – 12. Sustituyendo, obtenemos:

Simplificamos.

El discriminante es positivo ( nos da como resultado 49), así tenemos dos soluciones:

x = 4 y x = – 3
La gráfica que obtenemos es la siguiente:

como se puede observar sus puntos de intercepción con el eje (x) son (x= -3) y (x= 4).
MEDIANTE FACTORIZACIÓN
Como ya has visto la factorización nos brinda la posibilidad de simplificar una expresión algebraica hasta el punto de obtener por simple inspección sus raíces o soluciones posibles.
EJEMPLO
Trabajando con el ejemplo anterior:
x 2 – x – 12 = 0
Observamos que es un caso 6 de factorización, abrimos dos paréntesis y escribimos dos binomios cuyo primer término es la raíz cuadrada del primer término de la ecuación anterior. En el primer paréntesis es precedida por el signo menos que es el signo que acompaña el segundo término de la ecuación inicial. En el segundo paréntesis el signo depende de la multiplicación de los dos signos de la ecuación inicial, en este caso el resultado es positivo ( – por – nos da +).
(x – )(x + )
ahora debemos encontrar los segundos términos de los binomios anteriormente planteados; dos números que multiplicados nos den como resultado -12 y que restados nos den como resultado -1.
(x – 4)(x + 3) donde se cumple que (-4)(3)= 12 y -4 + 3 = -1
Cada expresión algebraica, o binomio para este caso representa una solución al problema, para obtener dicho resultado igualamos a cero cada binomio:
x – 4 = 0 de donde despejamos x = 4
x + 3 = 0 de donde despejamos x = -3
Que son los resultados a el problema.
OTROS GRADOS DE ECUACIONES
Para solucionar ecuaciones de grados mayores existen variados teoremas y ecuaciones para resolver, sin embargo puede ser considerado mas sencillo el método anterior.
MEDIANTE FACTORIZACIÓN PARA OTRAS ECUACIONES
ECUACIONES CÚBICAS y OTRAS
Revisa la ecuación, si tiene una letra constante entonces factoriza y transfórmala en una ecuación reconocida:
EJEMPLO
2x 3 +3x 2 – 2x Factorizamos caso 1
x(2x2 +3x – 2) Entre el paréntesis nos queda el caso 7 de factorización
x(x + 2)(2x – 1) Tenemos ahora tres raíces. Igualando a cero:
x = 0 primera solución
x + 2 = 0 despejando x = -2 segunda solución
2x – 1 = 0 despejando x = 1/2 = 0.5 tercera solución
Si graficamos la ecuación tenemos:

Donde las soluciones dadas son las intercepciones al eje x.
De igual forma puedes proceder con otros grados de ecuaciones.
Te dejo como interés que indagues la FORMULA DE TARTAGLIA-CARDANO.
FUNCIONES COMO REPRESENTACIONES GRÁFICAS
Como has observado últimamente, el concepto GRÁFICO de representación de la matemáticas adquiere un valor importante pues nos permite visualizar inmediatamente un resultado.
Conocer las principales formas representativas GRÁFICAS nos facilitaría el trabajo, por eso te invito a observar algunas de estas representaciones en forma de FUNCIONES.
Que importante es poder manejar y reconocer todos los elementos que una gráfica matemática te puede brindar como conocimiento. En este espacio estudiaremos algunas de ellas.
LA LINEA RECTA
De aquí en adelante cuando veas una expresión de uno o dos términos cuyo exponente es igual a la unidad, es decir de primer grado IMAGÍNATE UNA LINEA RECTA, una trayectoria lineal, una pelota que se deja caer desde una altura determinada o un vehículo que se desplaza en linea recta, las lineas que conforman un cuadrado u otra figura geométrica; etc.
De aquí en adelante cuando veas una expresión como 3x + 2 tu mente debe configurarla en una correspondencia con una realidad, como una FUNCIÓN, donde x es la variable independiente, mientras que y es la variable dependiente ( de los valores que tome x).
y = 3x + 2
Para su estudio, las ecuaciones de primer grado se pueden configurar así:
y = mx + b
El signo lo he tomado positivo para seguir con el ejemplo.
En esta función conoceremos a la letra m como la pendiente o grado de inclinación que tiene la linea recta; y la letra b como el punto de intercepción con el eje y.
Una pendiente (m) hace referencia al grado de inclinación o variación de y con respecto a x , que tiene la línea recta que pasa por dos puntos :

Tomado de: http://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funciones_elementales/teoria/interpolacion_lineal.html
Como puedes observar la variación se mide como la relación de espacio recorrido en el eje y por cantidad de espacio recorrido en el eje x. La gráfica nos muestra estos espacios en los catetos del triangulo rectángulo que se forma. El cateto adyacente es la variación en x mientra que el cateto opuesto es la variación en y.
y se calcula a partir de dos puntos sobre la recta mediante la siguiente ecuación:

En nuestro ejemplo el número 3 que es positivo representaría la letra m, es decir la pendiente y el número 2 positivo representaría la letra b es decir la intercepción con el eje y.
Grafiquemos la función y miremos otras cosas ( te recuerdo que para elaborar una gráfica en un plano cartesianos debes construir inicialmente una tabla de datos sustituyendo el valor de x por los datos que tu requieras, realizas la operación indicada y obtienes el valor de y; con esos pares de datos construyes tu gráfica) :

Analicemos esta gráfica:
- Al construirla es un linea recta
- Es una línea recta ascendente ( esto es debido a que el signo que acompaña la pendiente m para este caso es positivo (+3))
 Tomado de: http://matefacil01.blogspot.com.co/2011/05/funcion-lineal.html
Tomado de: http://matefacil01.blogspot.com.co/2011/05/funcion-lineal.html
3. Exactamente se corta el eje y en el punto 2 positivo ( tal como lo predecía la ecuación donde b= +2
4. Cuando x = -1 , entonces y = -1
5. Cuando x = -2 , entonces y = -4
6. Se forma un triangulo rectángulo ( en verde) que nos indica la variación de y con respecto a x, si aplicamos la ecuación de pendiente:
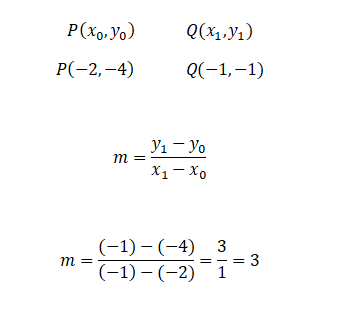
CONOCIENDO BÁSICAMENTE LA ESTADÍSTICA
Repasemos este tema de Octavo nuevamente. Teniendo en cuenta que la Estadística nos permite RECOLECTAR, ORGANIZAR, PROCESAR, ANALIZAR e INTERPRETAR datos, esta es entonces una gran herramienta de trabajo para la matemáticas de la Física.
Algunos conceptos básicos a tener en cuenta son:
POBLACIÓN: Que es el conjunto total de los elementos a estudiar. (EJEMPLO: los 5230 estudiantes del Colegio)
MUESTRA: Es una parte de la Población que sea representativa de los datos recolectados. (650 estudiantes seleccionados 10 de cada salón)
VARIABLE: Es la característica a medir. Las variables pueden ser:
CUALITATIVAS: Cuando no se pueden medir numéricamente y a su vez pueden ser : NOMINALES: cuando sus valores no se pueden ordenar (EJEMPLO: Sexo, grupo sanguíneo, religión; etc). ORDINALES: cuando sus valores se pueden ordenar ( Poco, muy poco, satisfecho, nada satisfecho, intensidad, etc)
CUANTITATIVAS: Cuanto poseen un valor numérico, se pueden clasificar en: DISCRETAS: cuando solo pueden tomar un valor numérico entero (EJEMPLO: número de hijos). CONTINUAS: Cuando pueden tomar cualquier valor real (EJEMPLO: la altura de las personas)
AGRUPACIÓN DE DATOS
Para facilitar el trabajo con los datos se suelen agrupar en cuadros de FRECUENCIAS. En nuestro caso manejaremos DOS tipos de AGRUPACIÓN:
-
AGRUPACIÓN SIMPLE:
En este tipo de agrupación los datos se transcriben en orden ascendente directamente en la tabla de frecuencias, un dato por cada fila de la tabla.


2. AGRUPACIÓN POR INTERVALOS:
En este caso se crean intervalos para agrupar los datos siguiendo el siguiente procedimiento:
- Se calcula el RANGO:

2. Se calcula el factor K:
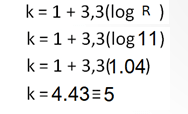
3. Se calcula la AMPLITUD O ANCHO DE CLASE:

De acuerdo a estos valores se elabora la tabla de la siguiente forma:

TIPOS DE FRECUENCIAS
Las frecuencias que emplearemos son:
FRECUENCIA ABSOLUTA:
Cantidad de veces que se repite el dato.
FRECUENCIA RELATIVA:
Cantidad porcentual del dato con respecto al total de datos.
Ambas frecuencias se pueden ACUMULAR o sumar en cada FILA. Al final la tabla de datos AGRUPACION SIMPLE queda de la siguiente forma:

en AGRUPACIÓN POR INTERVALO quedaría como:

FORMAS DE PRESENTACIÓN DE DATOS ESTADÍSTICOS
Para presentar de una forma visual y GRÁFICA los datos se emplean muchas formas de representación entre las cuales tenemos:
DIAGRAMA DE BARRAS
EJEMPLO: para nuestra frecuencia absoluta datos agrupación simple.

DIAGRAMA LINEAL
EJEMPLO: para nuestra frecuencia absoluta datos agrupación simple.

DIAGRAMA CIRCULAR
EJEMPLO : para nuestra frecuencia relativa datos agrupación simple.
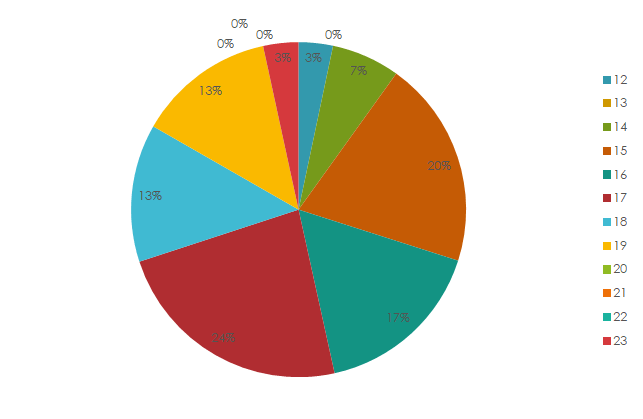
ANÁLISIS DE DATOS ESTADÍSTICOS
Existen diversos estudios para el análisis estadístico de datos. Inicialmente veremos los ESTUDIOS DE MEDIDAS DE TENDENCIA CENTRAL:




RECUPERACIÓN SEMESTRAL FINAL NOVENO
Para todos aquellos estudiantes que no alcanzaron el desarrollo total de sus competencias, se presentan a continuación los talleres de recuperación semestral. Cada taller consta de 2 sesiones o clases que están de acuerdo al cronograma. Para cada sesión es un taller que se debe presentar desarrollado, luego se dan las explicaciones del caso y por último se hace una evaluación por cada taller. La suma de todas estas evaluaciones dan la nota final.
TALLER RECUPERACIÓN SEMESTRAL 901
TALLER RECUPERACION SEMESTRAL 902
LOS TEXTOS A LEER EN LOS TALLERES SON LOS SIGUIENTES (DESCARGARLOS E IMPRIMIRLOS PARA SU PRESENTACIÓN):
1 TEXTO: La historia del Algebra en las aulas de Secundaria de Paula Albendea
2 TEXTO:Historia del algebra lineal hasta los albores del siglo XX de Deivi Luzardo
3 TEXTO:Las matemáticas y sus aplicaciones, ayer y hoy. Retos del futuro de Juan Luis Vázquez
4 TEXTO:Matemáticas aplicadas a la vida cotidiana y otros lugares inesperados de Alberto Vargas
5 TEXTO:Ecuaciones de Primer grado su historia. De Mario Dalcin
Para poder hacer las evaluaciones debe presentar los trabajos correspondientes.
NOTA: EL PRIMER CORTE SE REALIZARÁ EL 6 DE SEPTIEMBRE LA ASISTENCIA DE PADRES ES NECESARIA.
EL SEGUNDO CORTE SE REALIZARÁ EL 4 DE OCTUBRE
EN CADA CORTE SE REALIZARÁ ENTREGA DE TRABAJOS Y EVALUACIÓN DE COMPETENCIAS.
EL TRABAJO FINAL se realizará en este año el martes 6 de Noviembre de 2018 en la jornada tarde en las instalaciones del Colegio
Atte
TPJ